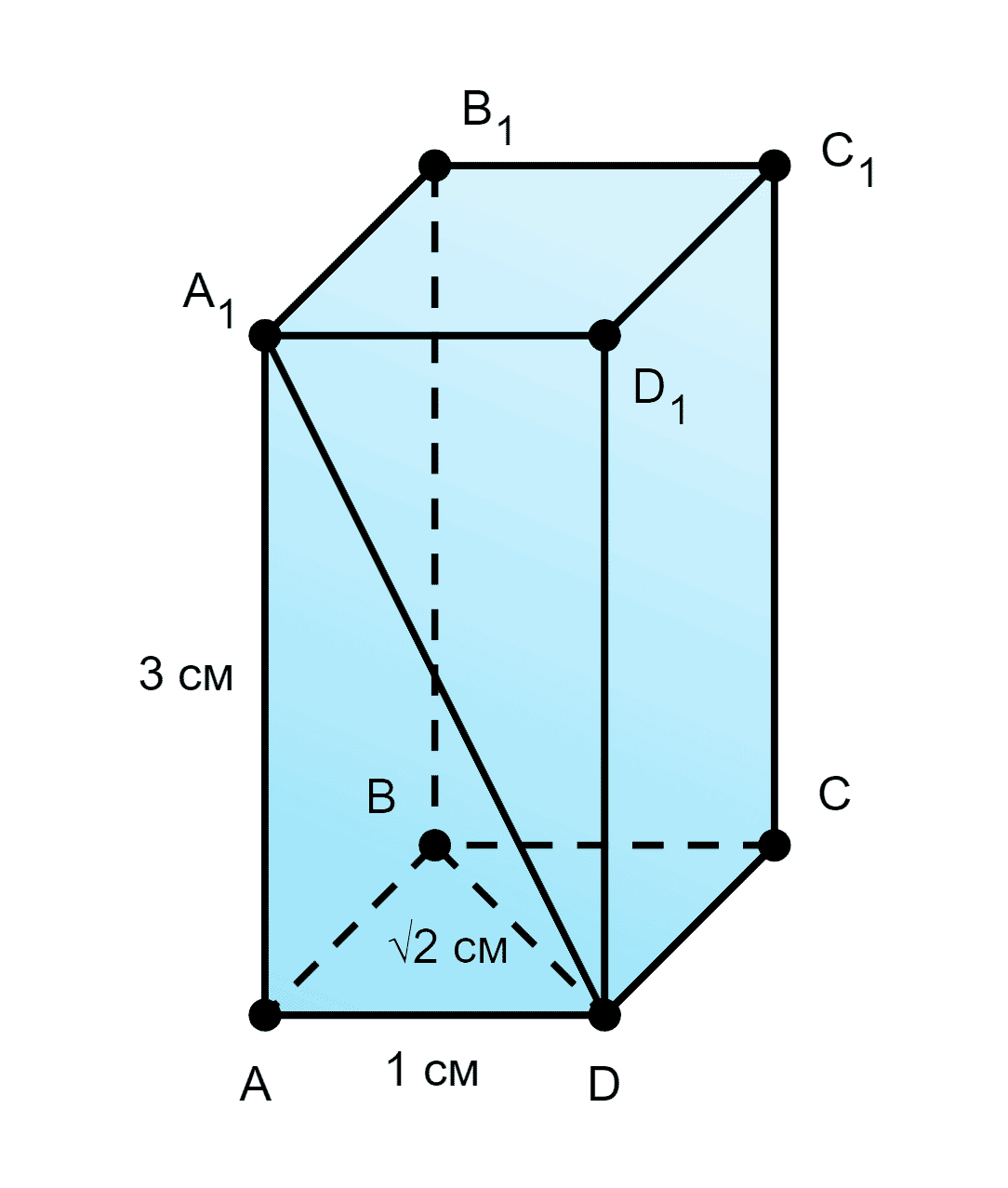
51. Боковая поверхность прямоугольного параллелепипеда с квадратным основанием равна 12 см^2 . Найдите диагональ боковой грани, учитывая, что диагональ основания равна √2 см.
Дано:
A B C D A 1 B 1 C 1 D 1 ABCDA_1B_1C_1D_1 A B C D A 1 B 1 C 1 D 1 — прямоугольный параллелепипед, A B C D ABCD A B C D — квадрат, S б о к = 12 с м 2 , S_{бок}=12\,см^2, S б о к = 1 2 с м 2 , B D = 2 с м . BD=\sqrt{2}\,см. B D = 2 с м .
Найти:
A 1 D A_1D A 1 D — ?
Решение:
1) Рассмотрим прямоугольный равнобедренный треугольник A B D ABD A B D с гипотенузой B D = 2 BD=\sqrt{2} B D = 2 . Его катеты равны 1 1 1 см: A D = A B = 1 с м . AD=AB=1\, см. A D = A B = 1 с м .
2) S A A 1 D 1 D = S б о к 4 ; S_{AA_1D_1D}=\dfrac{S_{бок}}{4}; S A A 1 D 1 D = 4 S б о к ;
Площадь одной боковой грани S = 3 с м 2 , S=3\, см^2, S = 3 с м 2 , следовательно боковая грань (прямоугольник) имеет размеры 1 1 1 см и 3 3 3 см:
S A A 1 D 1 D = A D ⋅ A A 1 ; S_{AA_1D_1D}=AD\cdot AA_1; S A A 1 D 1 D = A D ⋅ A A 1 ; A A 1 = S A A 1 D 1 D A D ; AA_1=\dfrac{S_{AA_1D_1D}}{AD}; A A 1 = A D S A A 1 D 1 D ;
A A 1 = 3 1 = 3 ( с м ) . AA_1=\dfrac{3}{1}=3\,(см). A A 1 = 1 3 = 3 ( с м ) .
3) A 1 D A_1D A 1 D — гипотенуза треугольника A 1 A D , A_1AD, A 1 A D , значит A 1 D 2 = A A 1 2 + A D 2 ; A_1D^2=AA_1^2+AD^2; A 1 D 2 = A A 1 2 + A D 2 ; A 1 D = A A 1 2 + A D 2 ; A_1D=\sqrt{AA_1^2+AD^2}; A 1 D = A A 1 2 + A D 2 ;
A 1 D = 3 2 + 1 2 = 9 + 1 = 10 ( с м ) . A_1D=\sqrt{3^2+1^2}=\sqrt{9+1}=\sqrt{10}\,(см). A 1 D = 3 2 + 1 2 = 9 + 1 = 1 0 ( с м ) .
A 1 D A_1D A 1 D — диагональ боковой грани параллелепипеда.
Ответ: 10 с м . \sqrt{10}\,см. 1 0 с м .