49. Имеется параллелепипед BCDEB1C1D1E1. Постройте:

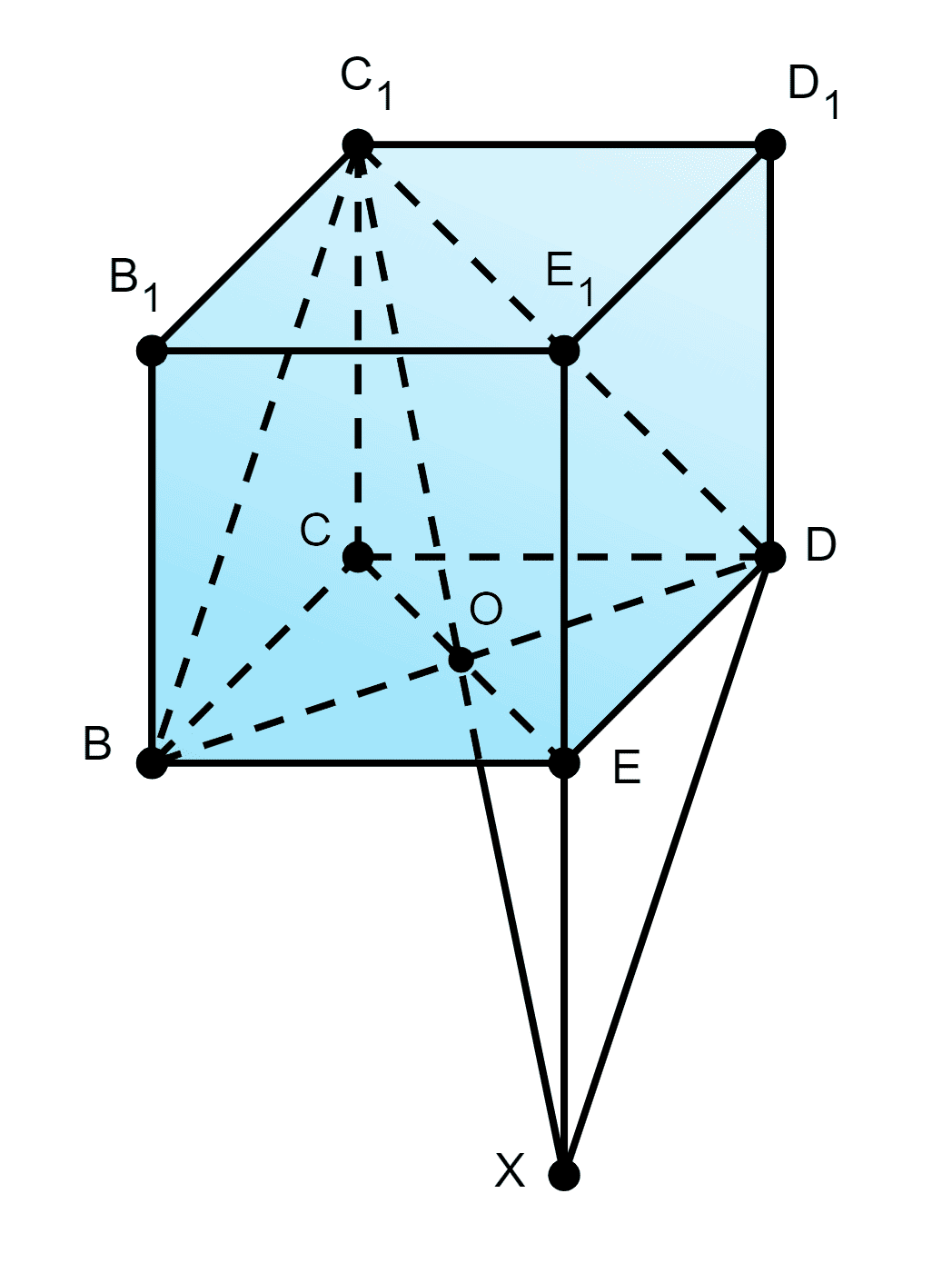
а) точку пересечения прямой $EE_1$ с линией пересечения плоскостей $BC_1D$ и $C_1CE.$

$(BC_1D)\cap (C_1CE)=C_1O,$

$EE_1\cap C_1O=X.$

Прямая и линия пересечения плоскостей пересекаются в точке $X.$

б) линию пересечения плоскостей $BC_1D$ и $EDD_1.$

$(BC_1D)\cap (EDD_1)=DX,$ т.к. $D\in (BC_1D); D\in (EDD_1); X\in (BC_1D)$ (см. пункт а)), $X\in (EDD_1)$ по Аксиоме 2.