46. Точки A и B — внутренние точки рёбер KM и KQ призмы KMOQK1M1O1Q1. Постройте:
а) точку, в которой прямая пересекает плоскость
Решение:
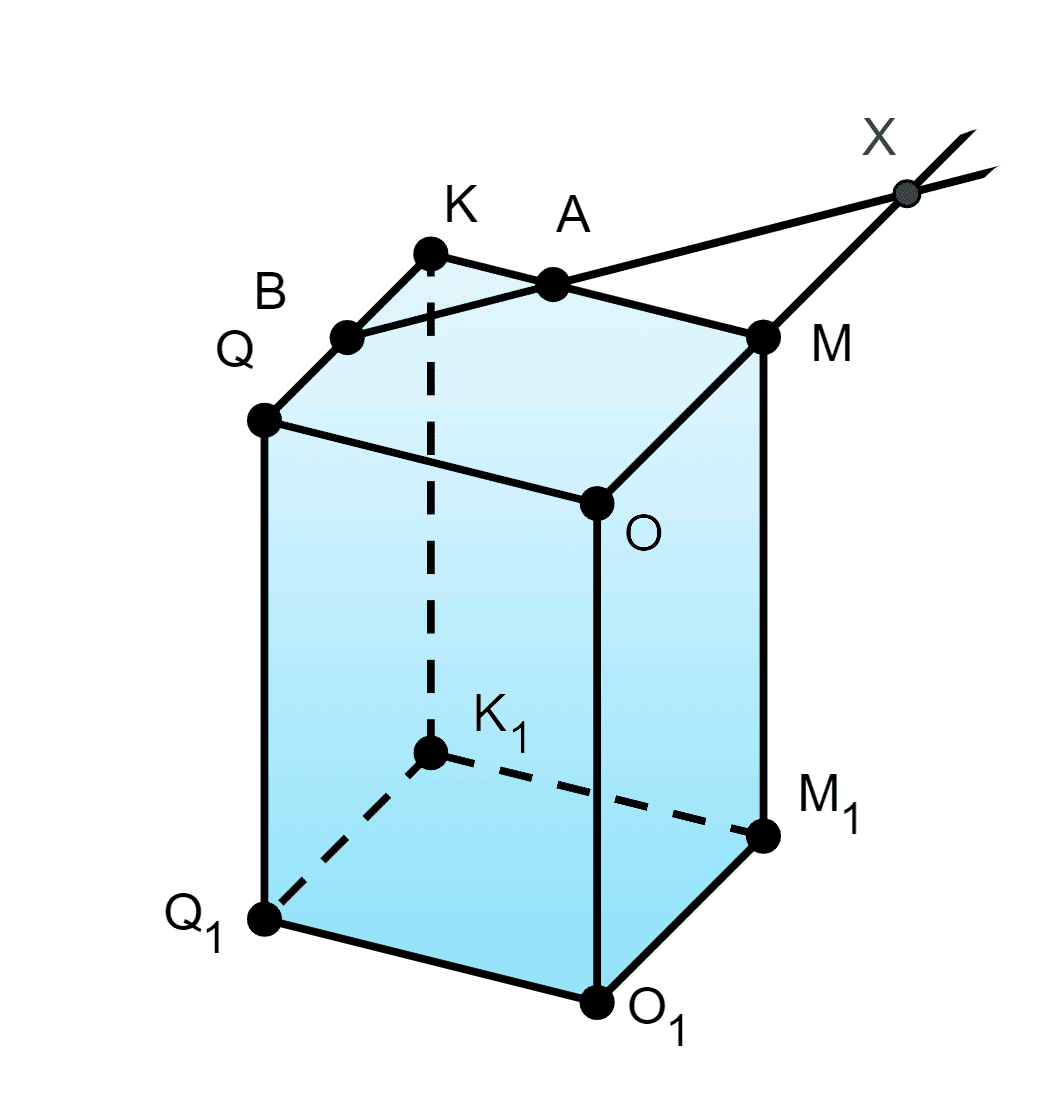
и — внутренние точки рёбер и следовательно прямые и не параллельны.
, значит
Прямая и плоскость пересекаются в точке
б) прямую, по которой плоскость пересекает плоскость
Решение:
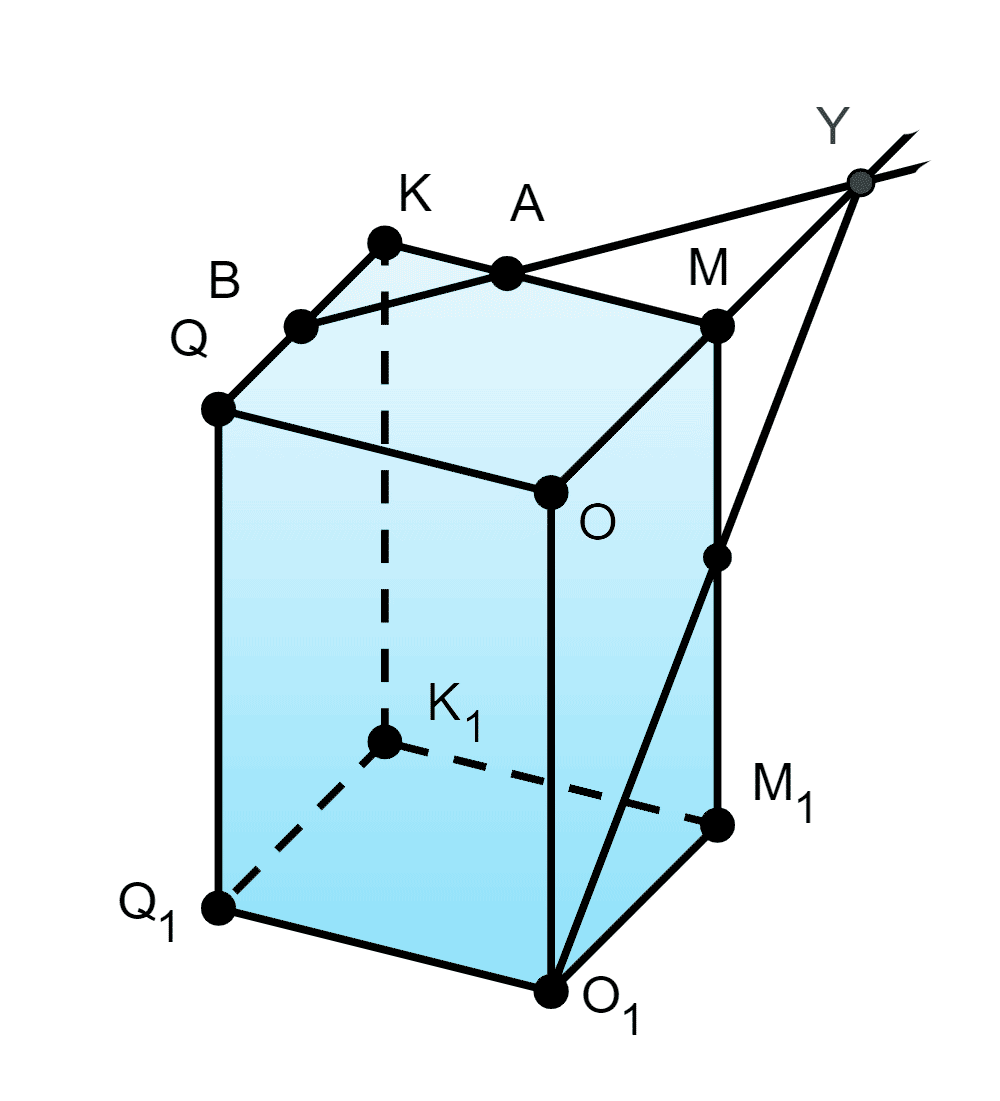
Находим
значит
Две плоскости пересекаются по прямой