43. Точки P, Q и R принадлежат соответственно рёбрам SA, SC и BC пирамиды SABCD (рис. 96). Постройте прямую, по которой плоскость PQR пересекает плоскость:

а) пересекает по $QR$:

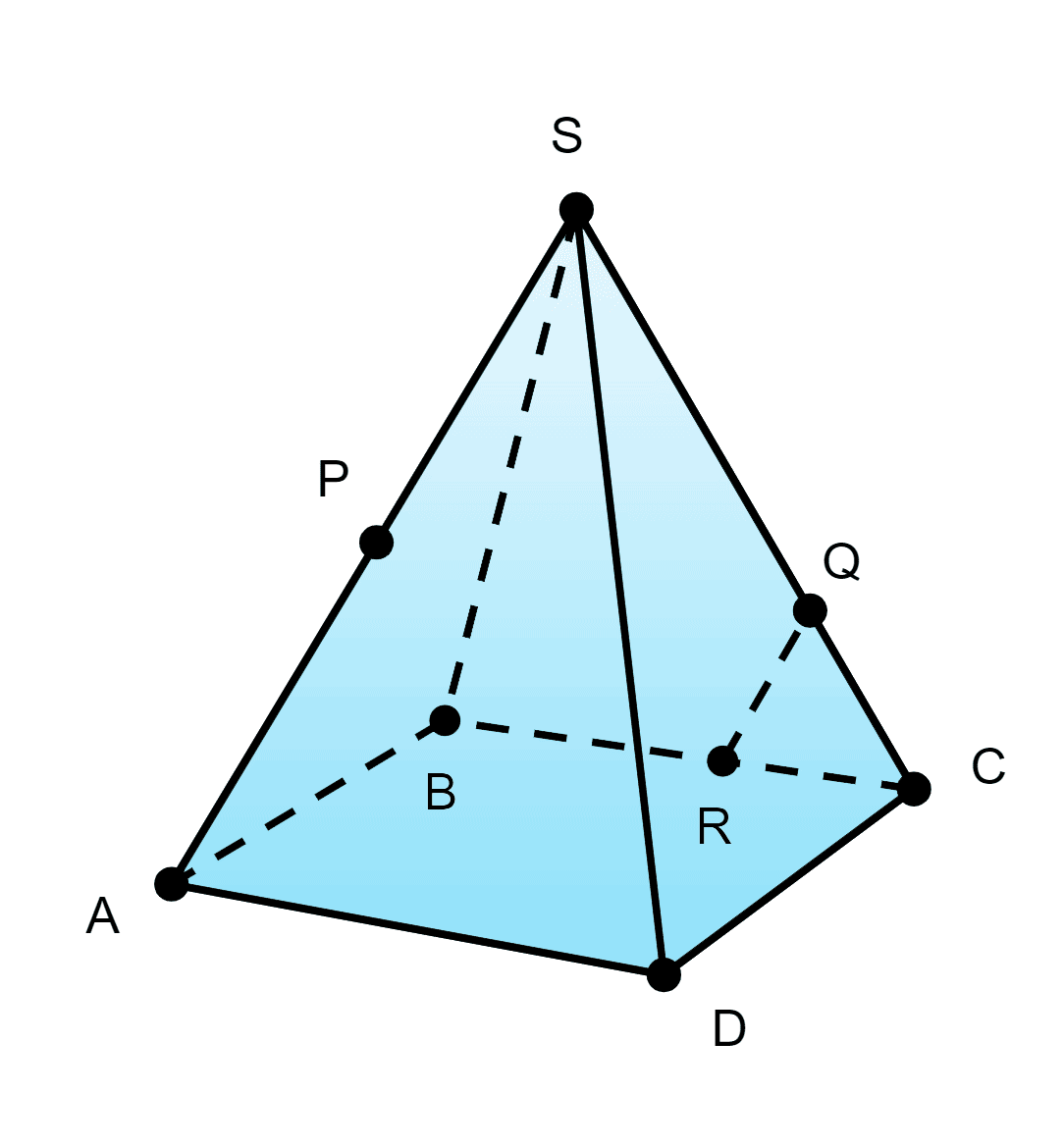
$(PQR)\cap (SBC)=QR$ по аксиоме 2.

б) пересекает по $PX$:

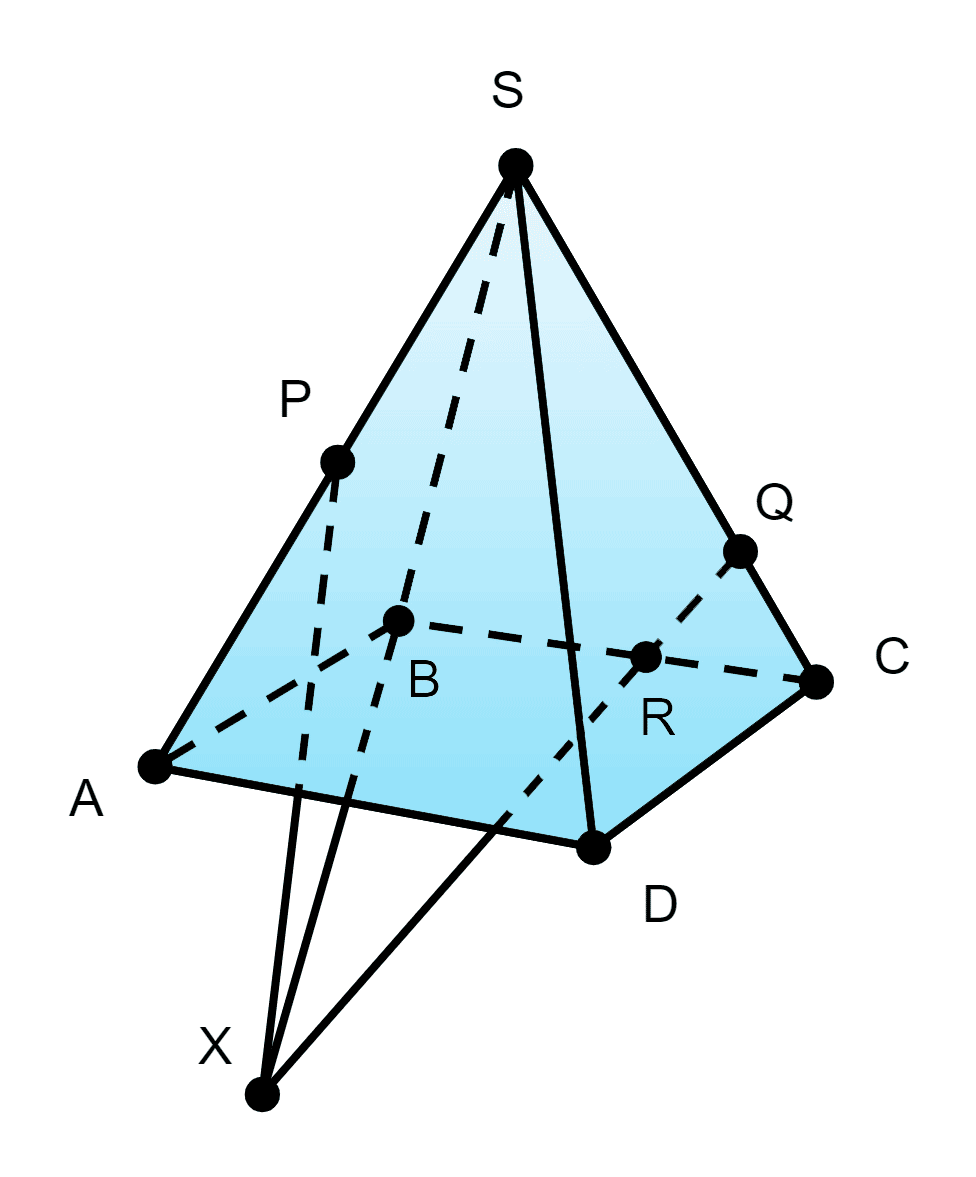
$(PQR)\cap (SAB)=PX$

$X=(QR)\cap (SB)$

Проведём $PX$

$PX\subset (PQR)$ и $PX\subset (SAB)$

в) пересекает по $SM$:

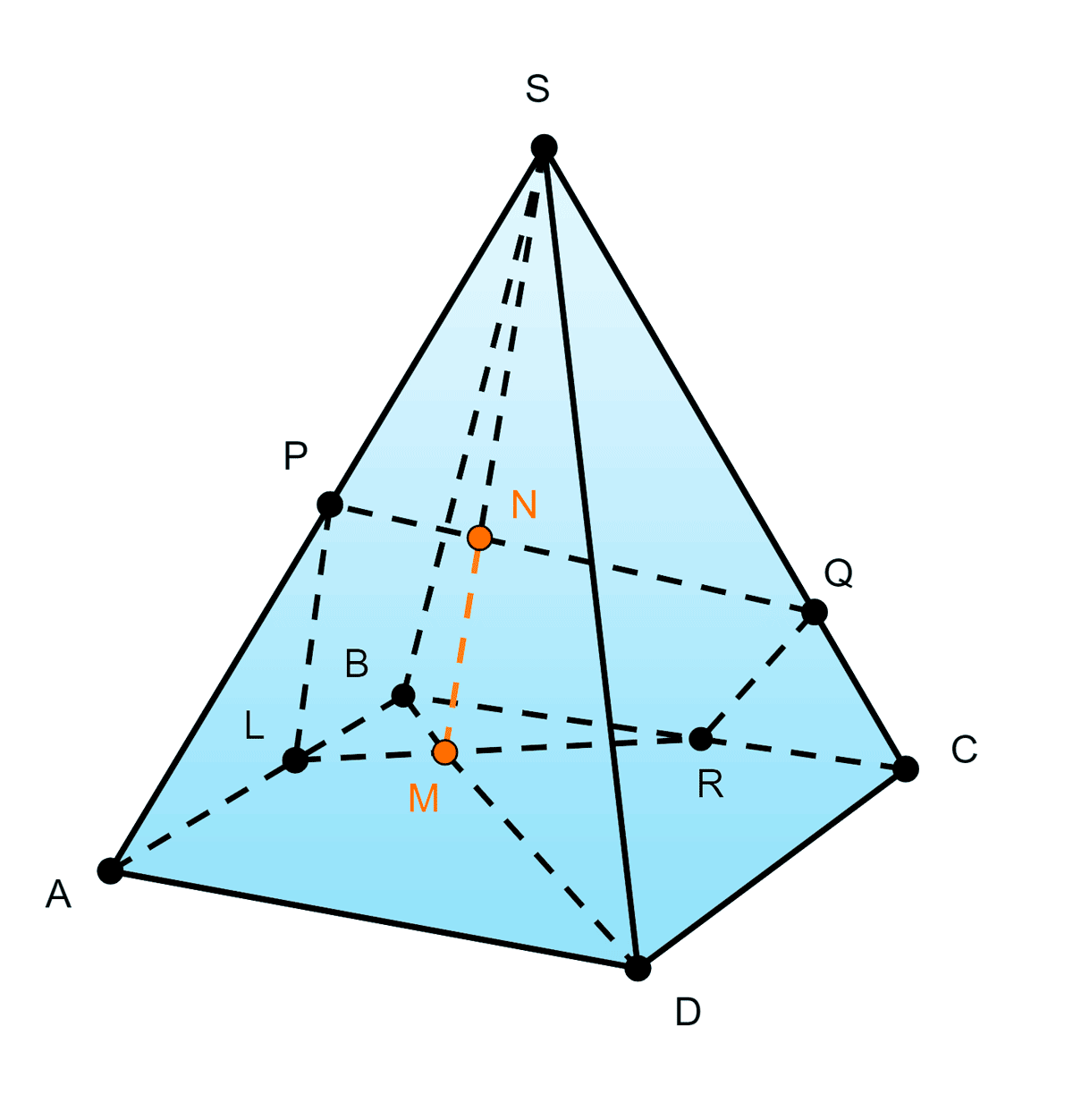
$(PQR)\cap (SBD), LR=(ABCD)\cap (PQR)$

$L=AB\cap PX; M=BD\cap LR$

$SM=NM=(PQR)\cap(SBD)$

г) Пересекает по $YQ$:

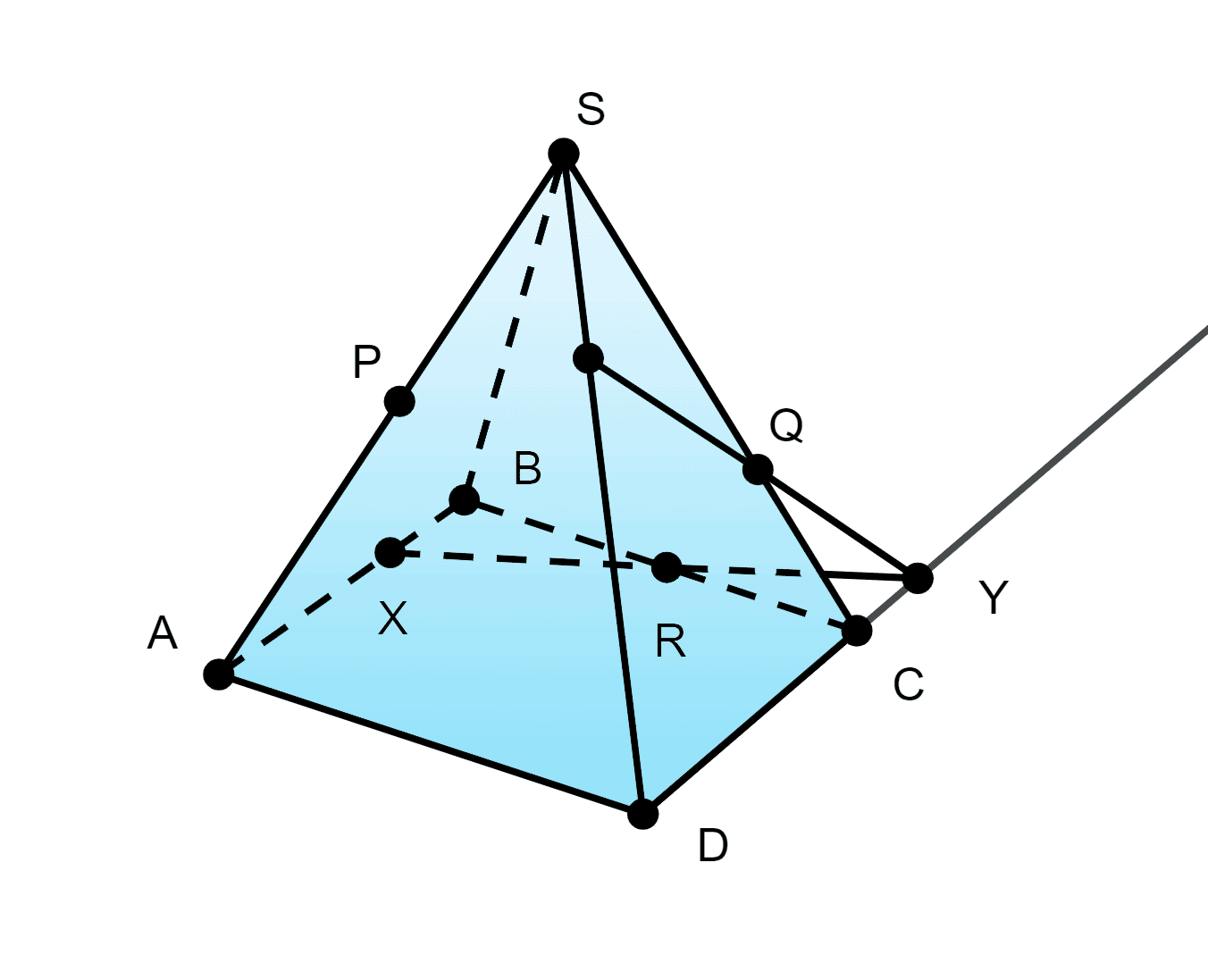
Находим точку $X=(PQR)\cap AB$ — см. пункт б)

$XR\cap CD=Y$ ($Y\in (PQR); Y\in (SDC)$)

$Q\in (SDC); Q\in (PQR),$ значит $YQ=(SDC)\cap (PQR).$