33. Плоскость β проходит через две смежные вершины трапеции и точку пересечения её диагоналей. Докажите, что две другие вершины трапеции лежат в плоскости β.

Решение:

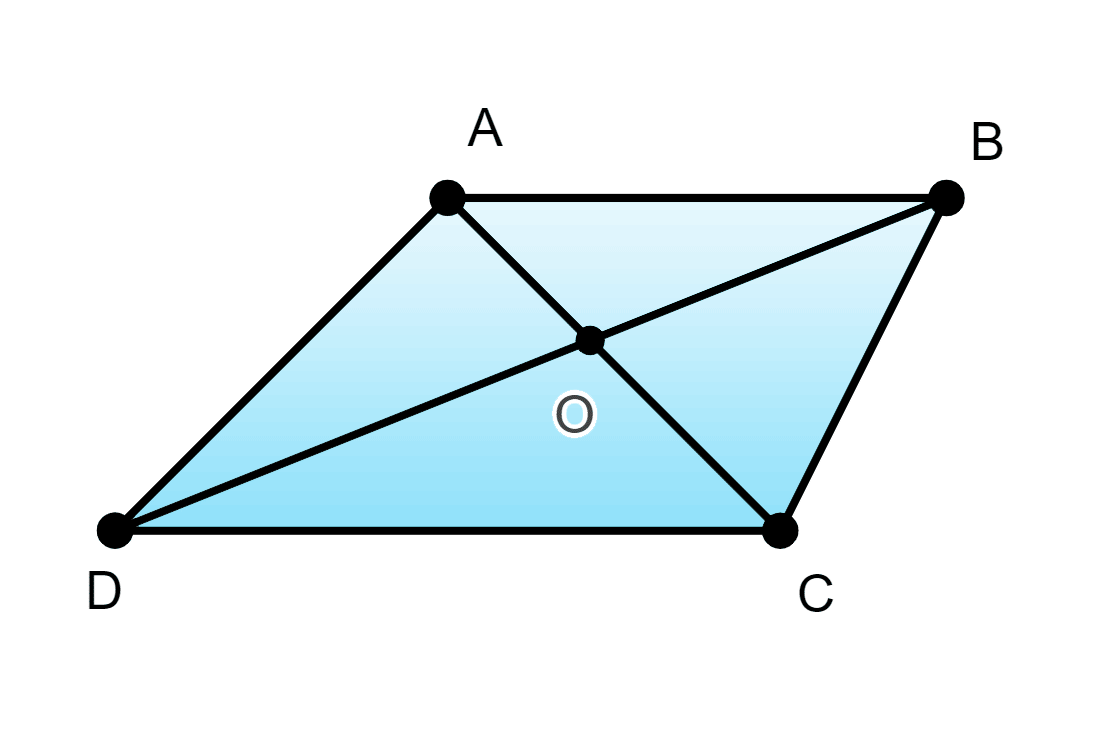
Пусть ABCDABCD — трапеция, O=AC∩BD;β=(AOB).O=AC\cap BD; \beta = (AOB).

Докажем, что C∈βC\in\beta и D∈β.D\in\beta. Т.к. A∈βA\in\beta и O∈β,O\in\beta, то по Аксиоме 2 следует, что AO∈AC⊂βAO\in AC\subset \beta (AOAO принадлежит AC,AC, которая принадлежит β\beta).

Аналогично BD⊂β,BD\subset\beta, значит C∈βC\in\beta и D∈β.D\in\beta.