32. Докажите, что любая прямая, которая:

а) проходит через вершину A треугольной пирамиды ABCD и пересекает прямую CD, принадлежит плоскости ACD;

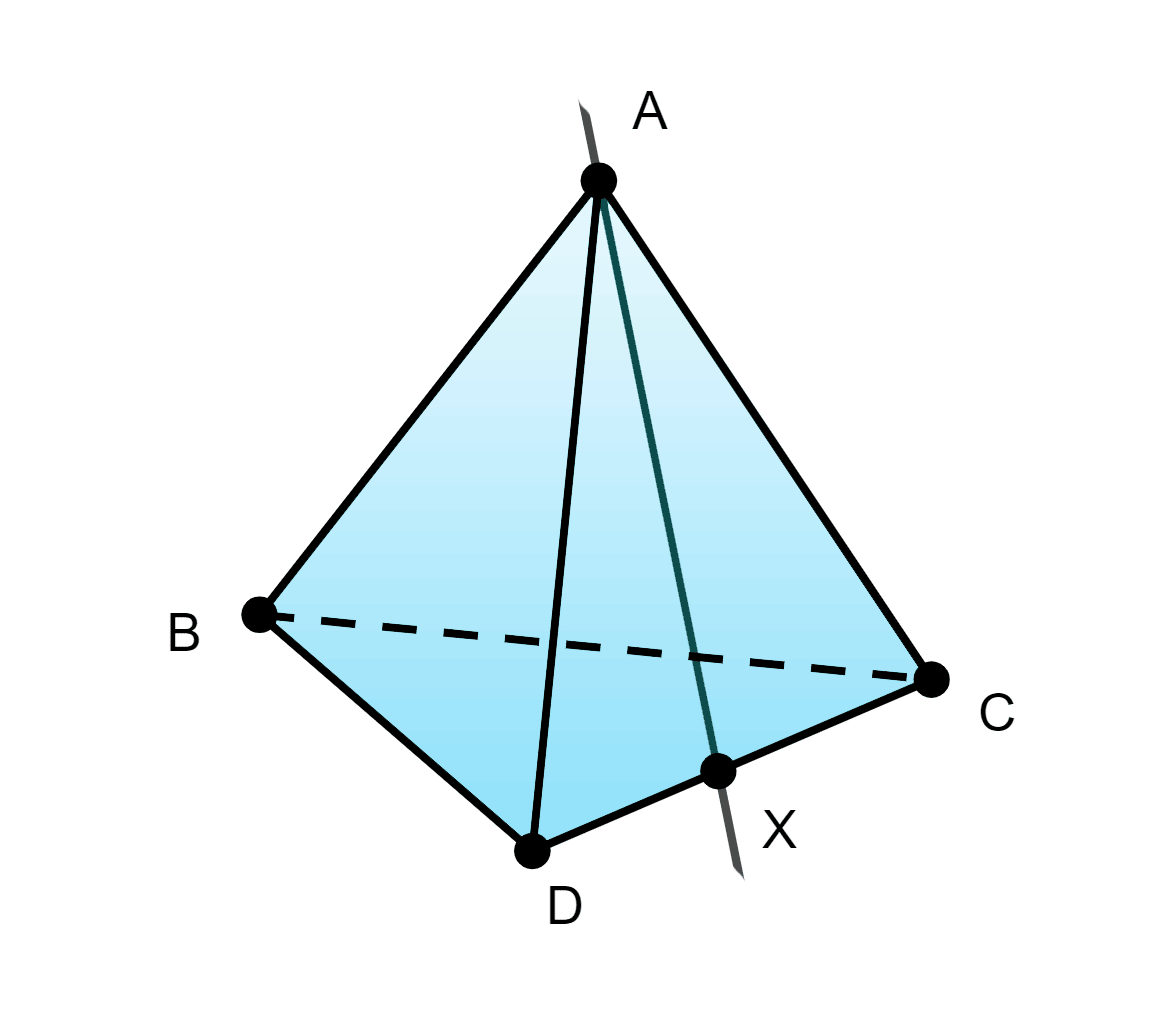
Решение:

Пусть $a=AX,$ т.к. $A\in(ACD)$ и $X\in (ABC), X=AX\cap CD,$ то по Аксиоме 2 $AX\subset(ACD)$, т.е. $a\subset(ACD).$

Подробно. Пусть $a=AX;$ т.к. $A$ и $X$ принадлежат $ACD$ и $AX$ пересекает $CD$ в точке $X,$ то по Аксиоме 2 (если две точки прямой лежат в плоскости, то каждая точка этой прямой принадлежит плоскости) $AX$ принадлежит $ACD,$ значит и $a$ принадлежит плоскости $ACD.$

б) не проходит через вершину B треугольной пирамиды ABCD и пересекает как прямую BC, так и прямую BD, принадлежит плоскости BCD.

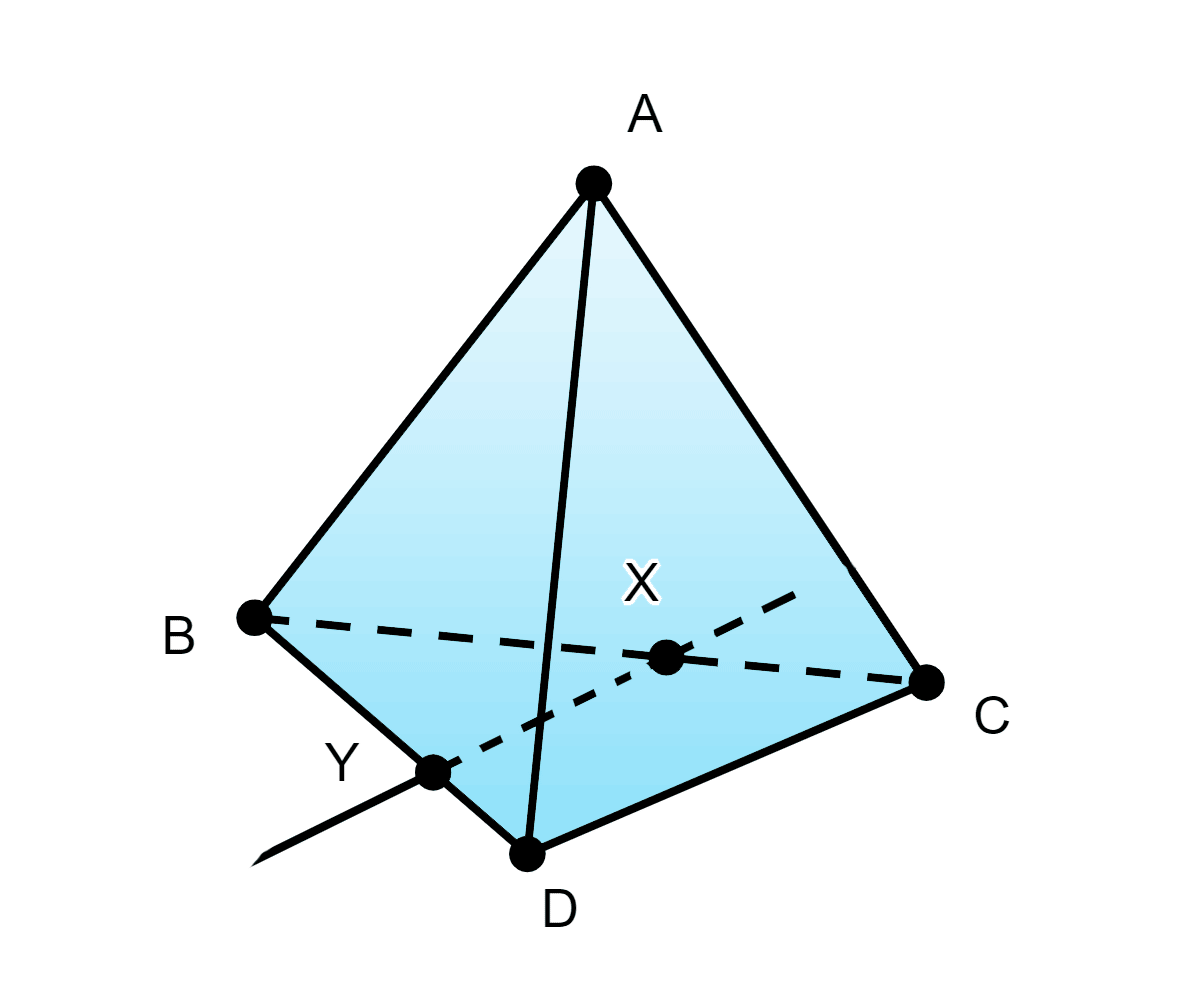
Решение:

Пусть $a=XY: B\notin a; X=a\cap BC; Y=a\cap BD,$ т.к $X\in BC\subset BCD, Y\in BD\subset BCD,$ то по Аксиоме 2 $a\subset (BCD).$

Подробно. Пусть $a=XY,$ тогда $B$ не принадлежит $a;$ $X$ является точкой пересечения прямых $a$ и $BC;$ $Y$ является точкой пересечения прямых $a$ и $BD.$ Т.к. $X$ принадлежит $BC,$ а $BC$ принадлежит $BCD,$ $Y$ принадлежит $BD,$ а $BD$ принадлежит $BCD,$ то по Аксиоме 2 $a$ принадлежит плоскости $BCD.$