30. Докажите, что если две смежные вершины четырёхугольника и точка пересечения его диагоналей принадлежат некоторой плоскости, то четырёхугольник целиком лежит в этой плоскости.

Решение:

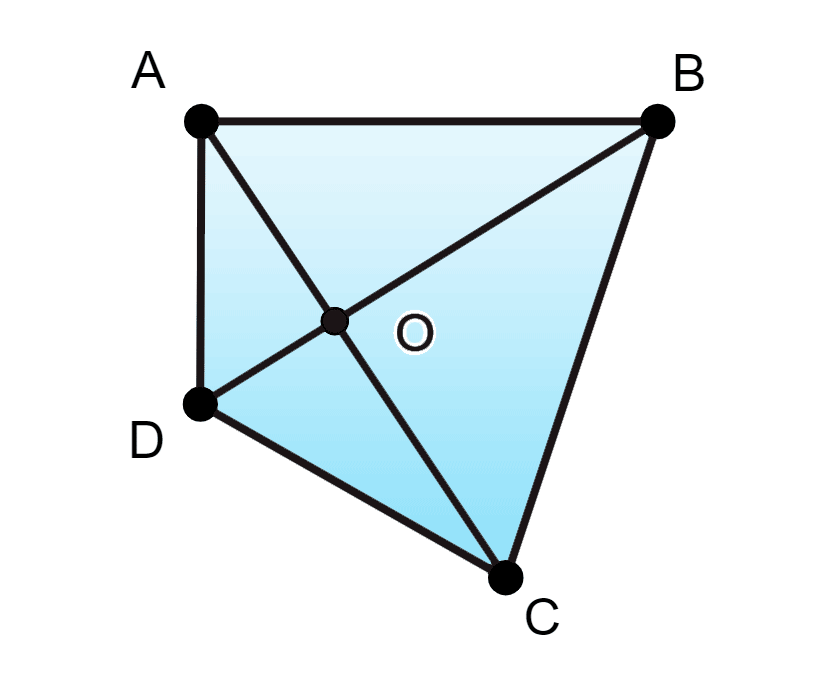
Пусть ABCDABCD — четырёхугольник, α\alpha — некоторая плоскость, A∈α,B∈α,O∈α,(O=AC∩BD).A\in \alpha, B\in \alpha, O\in \alpha, (O=AC\cap BD).

По Аксиоме 2:

A∈α;B∈α⇒AB⊂α;A\in \alpha; B\in\alpha \Rightarrow AB\subset\alpha;

A∈α;O∈α⇒AO=AC⊂α⇒C∈α;A\in \alpha; O\in\alpha \Rightarrow AO=AC\subset\alpha \Rightarrow C\in\alpha;

B∈α;O∈α⇒BO=BD⊂α⇒D∈α.B\in\alpha; O\in\alpha \Rightarrow BO=BD\subset \alpha \Rightarrow D\in \alpha.

Значит BC;CDBC; CD и ADAD принадлежит α,\alpha, т.е. четырёхугольник ABCDABCD целиком лежит в плоскости α.\alpha.