16. Основанием пирамиды QABCD является ромб ABCD со стороной, равной 10 см, одна из диагоналей которого равна 16 см. Отрезок, соединяющий вершину Q пирамиды с точкой O пересечения диагоналей основания, перпендикулярен этим диагоналям и равен 14 см (рис. 47). Найдите:

а) боковые рёбра пирамиды;

б) боковую поверхность пирамиды.

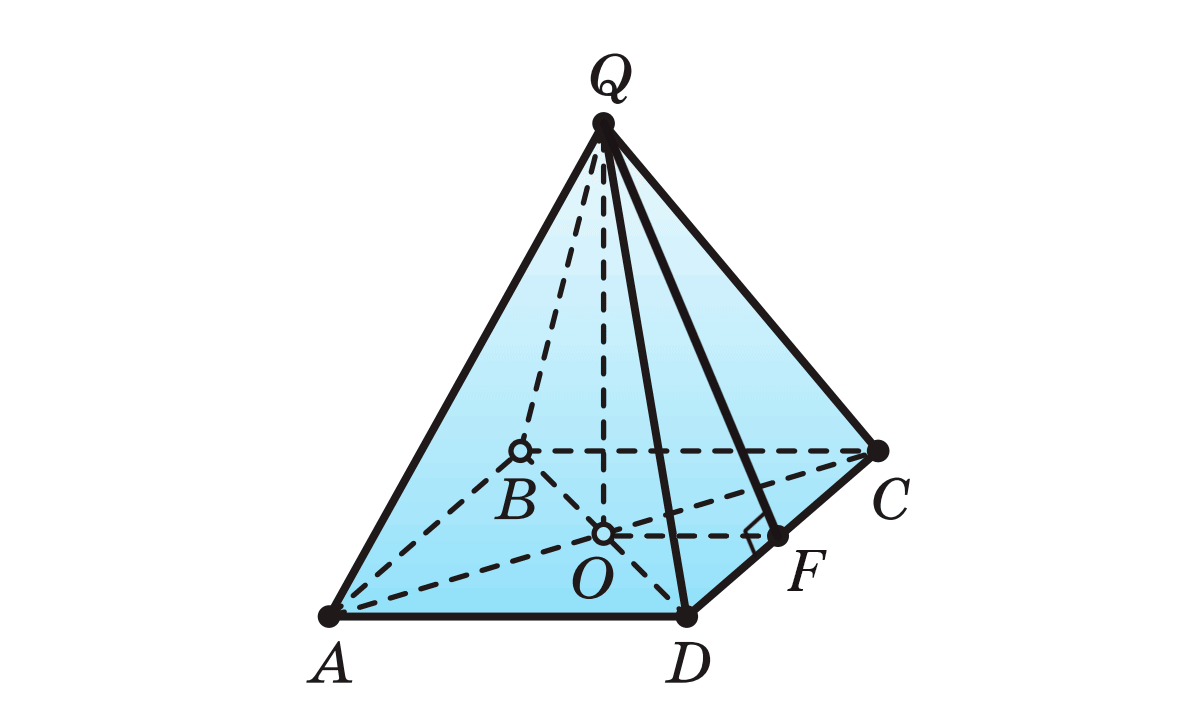
Решение:

Пусть $QABCD$ — пирамида, $ABCD$ — ромб, $AB=10$ см, диагональ основания $AC=16$ см, $QO=14$ см, $O$ — точка пересечения диагоналей основания пирамиды, $QO\perp AC$ и $QO\perp BD.$ Найдём:

а) боковые рёбра пирамиды. Находим другую диагональ ромба используя равенство $d_1^2+d_2^2=2a^2+2b^2.$

Тогда $BD^2=4AB^2-AC^2;$

$BD^2=400-256=144; BD=12$ см.

Для нахождения рёбер пирамиды воспользуемся прямоугольными треугольниками $AOQ$, $BOQ$ и теоремой Пифагора, а также свойством диагоналей параллелограмма ($AO=OC; BD=OD$).

Боковое ребро $AQ=CQ=\sqrt{8^2+14^2}=\sqrt{260}=2\sqrt{65}$ см.

Боковое ребро $BQ=QD=\sqrt{6^2+14^2}=\sqrt{232}=2\sqrt{58}$ см.

Б) Боковую поверхность пирамиды составляют четыре равных треугольника, для нахождения площади боковой грани нужно найти высоту $QF$ треугольника $DQC.$

Рассмотрим треугольник $QOF$: $\angle{QOF}=90°; QO=14$ см, $OF=r$ — радиус вписанной в ромб окружности.

По формуле $S=p\cdot r$ находим $p$ — полупириметр ромба:

$r=\dfrac{S}{p}, p=\dfrac{40}{2}=20$ см; $S=\dfrac{d_1\cdot d_2}{2}=\dfrac{16\cdot 12}{2}=96$ см$^2.$

$r=\dfrac{96}{20}=4.8$ см. $OF=r=4.8$ см.

По теореме Пифагора находим $QF=\sqrt{QO^+OF^2}=\sqrt{196+23.04}=\sqrt{219.04}=14.8$ см.

$S_{бок}=4\cdot S_{DQC};$

$S_{DQC}=\dfrac{1}{2}\cdot 10\cdot 14.8=74$ см.

$S_{бок}=296$ см.

Ответ: а) $2\sqrt{58}$ см; $2\sqrt{65}$ см; б) $296$ см$^2.$