Практ. 4

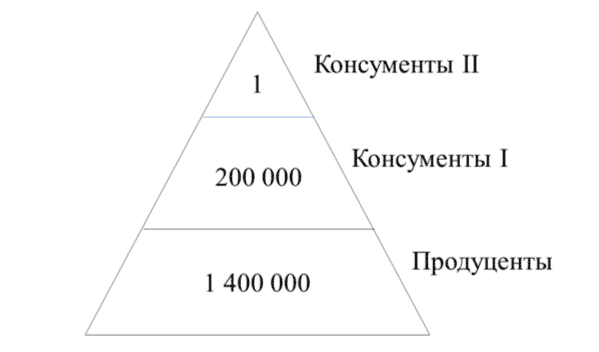
1. Постройте экологическую пирамиду чисел для степи (летом), если количество особей, кроме микроорганизмов и почвенных животных, на 1000 м2 составляет: продуцентов — 1 400 000; консументов I порядка — 200 000; консументов II порядка — 1.

2. Сколько потребуется растений, чтобы в лесу вырос волк и смог достичь массы 40 кг? Пищевая цепь: растения → заяц → волк.

40 кг волка — это 10 % биомассы от зайцев, которые необходимы для волка, а масса зайцев — это 10% биомассы растений, которые нужны, чтобы прокормить всех зайцев. Соответственно масса зайцев 40х100/10 = 400 кг. 400 кг зайцев необходимо волку. Масса растений — это 400х100/10 = 4000 кг. Это масса растений, необходимая для 400 кг зайцев.

3. Используя правило перехода энергии с одного трофического уровня на другой (правило 10%), постройте пирамиды биомассы и численности для следующей пищевой цепи луга: растения → кузнечик → лягушка → уж → змееяд. Данные для работы: биомасса всех растений луга — 400 000 кг; одного побега травянистого растения — 5 г (0,005 кг); кузнечика — 1 г (0,001 кг); лягушки — 10 г (0,01 кг); ужа — 100 г (0,1 кг); змееяда — 2 кг.

Пирамида биомассы

Пирамида биомассы

4. Рассмотрите пищевую цепь: злаки → кузнечики → лягушки → змеи → орлы. Определите биомассу злаков (в тонах), необходимую для того, чтобы суммарный прирост биомассы птиц за год составлял 20 кг, если известно, что в 1 кг растений аккумулируется 100 кДж энергии, а 1 кг биомассы птиц соответствует 20 кДж.

1 кг птиц — 20 кДж, а 20 кг птиц — 400 кДж. Переходя от птиц к злакам по трофическим уровням и применяя обратное правило Линдемана, мы высчитали, что для того, чтобы птицам дошло 400 кДж энергии, нам необходимо 4 000 000 кДж энергии от злаков.

Орлы — 400 кДж
Змеи — 4 000 кДж
Лягушки — 40 000 кДж
Кузнечики — 400 000 кДж
Злаки — 4 000 000 кДж

1 кг злаков — 100 кДж, а 4 000 000 кДж — это 40 000 кг.

Ответ: 40 000 кг (40 тонн) злаков.

5. Одна мышь биомассой 5 г рождает двух детёнышей массой 1 г и 0,5 г. За 3-4 недели выкармливания детёнышей молоком их масса составит 5 г и 4 г соответственно. На основании правила экологической пирамиды определите, какая биомасса зерна необходима самке, чтобы выкормить своё потомство.

В данном случае детёныши мыши не будут участниками пищевой цепи, т. к. мышь их не ест. Поэтому мы считаем, что прирост для мышат равен приросту для матери. Пищевая цепь будет выглядеть следующим образом:

зерно → мышь

Сумма исходных масс мышат равна 1,5 г., а их масса после выкармливания равна 9 г. Соответственно прирост будет равен 7,5 граммам (9-1,5 = 7,5).

По обратному правилу Линдемана 7,5 граммам мышат соответствует 75 граммов зерна.

Ответ: 75 граммов.

6. На определённой территории живут зайцы, биомасса каждого из них отличается на 0,2 кг. Биомасса самого маленького зайца — 1,6 кг, а самого большого — 5 кг. Масса одной лисицы в 20 раз меньше суммарной массы всех зайцев, найдите среднюю одной лисы. Вычислите, сколько лис могут существовать на данной территории, если они питаются только зайцами.

Пищевая цепь: заяц → лиса.

Суммарная масса всех зайцев равна 59,4 кг. (1,6 + 1,8 + 2 …+ 4,8 + 5).

Средняя масса лисы в 20 раз меньше массы всех зайцев. Значит средняя масса одной лисы = 59,4/20 = 2,97 кг.

По правилу Линдемана биомасса лис равно 5, 94 кг. (10% от 59,4 кг.)

Количество лис = 5, 94/2,97 = 1,93 ≈ 2.

Ответ: средняя масса лисицы = 2, 97 кг; 2 лисы могут существовать на данной территории.

7. Рассчитайте количество консументов III порядка в лесу, где энергия всех продуцентов составляет 1000 кДж. Известно, что одна особь искомых консументов весит 100 г, а в 1 кг массы запасается 1000 Дж энергии.

Пищевая цепь:

Продуценты → КI → КII → КIII.

По правилу Линдемана до Консументов III доходит 1 кДж
Продуценты – 1000 кДж
КI – 100 кДж
КII – 10 кДж
КIII – 1 кДж
1 кДж = 1000 Дж = 1 кг массы КIII
1 особь – 100г. 1 кг (1000г) / 100г = 10 особей

Ответ: 10 особей.

8. Сделайте вывод о практическом значении правила Линдемана.

Используя это правило, можно рассчитать примерное количество энергии на любом трофическом уровне цепи питания, если её показатель известен хотя бы на одном из них. А практическое значение правила Линдемана очень невелико. Оно соблюдается в экосистеме только при наличии оптимальных условий среды и полной обеспеченности кормом