Лаб. 4
4. Выполните задание 3, подвесив к пружине поочередно два, три, четыре груза. Измерьте соответствующие абсолютные удлинения пружины и их средние значения.
$\langle x\rangle=\frac{0.03+0.03+0.03}{3}=0.03$ м;
$x_1=0.03$ м; $x_2=0.03$ м; $x_3=0.03$ м;
$\langle x\rangle=\frac{0.05+0.05+0.05}{3}=0.05$ м;
$x_1=0.05$ м; $x_2=0.05$ м; $x_3=0.05$ м;
$\langle x\rangle=\frac{0.078+0.078+0.078}{3}=0.078$ м;
$x_1=0.078$ м; $x_2=0.078$ м; $x_3=0.078$ м;
$\langle x\rangle=\frac{0.1+0.1+0.1}{3}=0.1$ м;
$x_1=0.1$ м; $x_2=0.1$ м; $x_3=0.1$ м;
5. Используя метод подсчёта цифр (см. приложение 2), рассчитайте модуль силы упрyгости пружины при подвешивании одного, двух, трех и четырех грузов. Занесите данные расчетов в таблицу.
$F = 0,2$ кг $⋅ 9,81 = 1,962$ Н;
$F = 0,3$ кг $⋅ 9,81 = 2,943$ Н;
$F = 0,4$ кг $⋅ 9,81 = 3,924$ Н.
| Кол-во грузов | Масса груза | Сила упр. | Абсолютное удлинение $x$ | |||
| Повторные измерения | ||||||
| $x$ | $x$ | $x$ | $\langle x\rangle$ | |||
| $1$ | $0.1$ | $1$ | $0.03$ | $0.03$ | $0.03$ | $0.03$ |
| $2$ | $0.2$ | $2$ | $0.05$ | $0.05$ | $0.05$ | $0.05$ |
| $3$ | $0.3$ | $3$ | $0.078$ | $0.078$ | $0.078$ | $0.078$ |
| $4$ | $0.4$ | $4$ | $0.1$ | $0.1$ | $0.1$ | $0.1$ |
6. Для нахождения среднего значения жесткости пружины постройте график зависимости модуля силы упругости от среднего удлинения при различном количестве грузов.
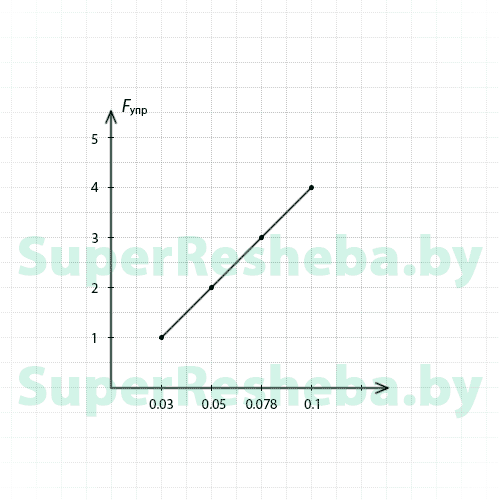
9. Результат прямых измерений x запишите в интервальной форме.
$\langle k\rangle=\dfrac{F_y}{x};$
$\langle k\rangle=\dfrac{2}{0.05} = 40$ Н.
10. Ответьте письменно на контрольные вопросы
1.
Вес приложен к пружине, а сила упругости приложена к центру масс тела.
За исправления спасибо Кираму.
2.
Нет. Количество грузов не влияет на область действия закона Гука. Если продолжать удлинять материал, произойдёт пластическая деформация, в которой уже не будет выполняться прямая пропорциональная зависимость.
Выводы: если к пружине подвесить груз массой, то под действием груза пружина удлиняется. На покоящийся относительно пружины груз действуют две компенсирующие друг друга силы — тяжести и упругости.
11. Суперзадание
Уменьшится жёсткость. Представим, что пружина — это несколько пружин, собранных последовательно. Если учесть соотношение $\dfrac{1}{c_0} = \dfrac{1}{c_1} = \dfrac{1}{c_2}$, где $c_0$ — жёсткость начальной пружины, $c_1$ — жёсткость удалённой части, $c_2$ — жёсткость конечной пружины, то можно определить, во сколько раз она увеличивается. Жёсткость станет $\dfrac{3}{2}$ от той, что была изначально.