Практ. 3
1. Определите, что изображено на рисунке:
Сеть питания, тип возрастной пирамиды популяции животного, цепь питания, экологическая пирамида (нужное подчеркните).
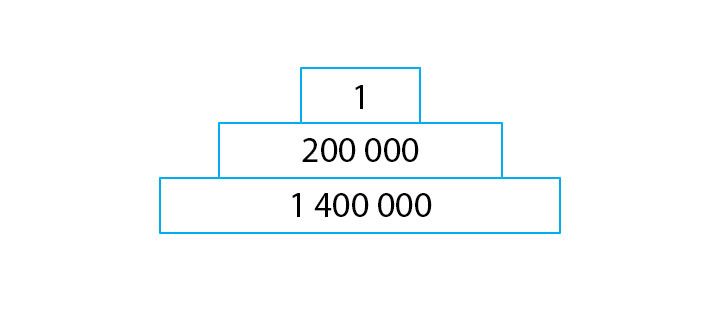
2. Постройте экологическую пирамиду чисел для степи (летом), если количество особей, кроме микроорганизмов и почвенных животных, на 1000 м^2 составляет: продуцентов — 1 400 000; консументов первого порядка (растительноядных животных) — 200 000; консументов второго порядка (хищников) — 1. Масштаб изображения произвольный
3. Сколько потребуется растений, чтобы в лесу вырос волк и смог достичь массы 40 кг? Пищевая цепь: растения → заяц → волк
Растения → заяц → волк
4000 кг → 400 кг → 40 кг
4. Используя правило перехода энергии с одного трофического уровня на другой (правило 10%), постройте пирамиды биомассы и численности для следующей пищевой цепи луга: растения → кузнечики → лягушки → ужи → змееяд. Данные для работы: биомасса всех растений луга - 40 000 кг; одного побега травянистого растения - 5 г (0.005 кг); кузнечика - 1 г (0.001 кг); лягушки - 10 г (0.01 кг); ужа - 100 г (0.1 кг); змееяда - 2 кг.
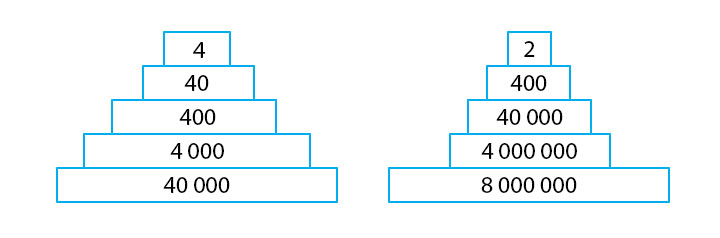
Пирамида 1 — биомассы; пирамида 2 — численности.
5. Рассмотрите пищевую цепь: злаки → кузнечики → лягушки → змеи → орлы. Определите биомассу злаков (т), необходимую для того, чтобы суммарный прирост биомассы птиц за год составил 20 кг, если известно, что в 1 кг растений аккумулируется 100 кДж энергии, а 1 кг биомассы птиц соответствует 20 кДж.
- 20 · 20 = 400 (кДж — энергии аккумулирует 20 кг биомассы птиц).
- 4 млн : 100 = 4000 (кДж — должны аккумулировать злаки).
6. Одна мышь биомассой 5 г рожает двух детенышей массой 1 г и 0.5 г. За 3-4 недели выкармливания детенышей молоком их масса становится 5 г и 4 г соответственно. На основании правила экологической пирамиды определите, какая биомасса зерна необходима самке, чтобы выкормить свое потомство.
- Зерно → мышь;
- масса, набранная детёнышами: 4 + 3 = 7 (г);
- 7 · 10 = 70 (грамм — зерна мыщь должна потребить).
7. На определенной территории живут зайцы, биомасса каждого из них отличается на 0.2 кг. Биомасса самого маленького зайца - 1.6 кг, а самого большого - 5 кг. Масса одной лисы в 20 раз меньше суммарной массы всех зайцев. Найдите среднюю массу одной лисы. Вычислите, сколько лис могут существовать на данной территории, если они питаются только зайцами.
- 1.6 кг до 5 кг (с шагом в 0.2 кг) = 60 кг (18 зайцев);
- 60 : 20 = 3 (кг — масса одной лисы);
- зайцы → лисы;
- 6 : 3 = 2 (количество лис, которые могут существовать на данной территории).