Контр. 7. Подобные фигуры
1. Используя данные рисунка, укажите верное утверждение:
Вариант 1
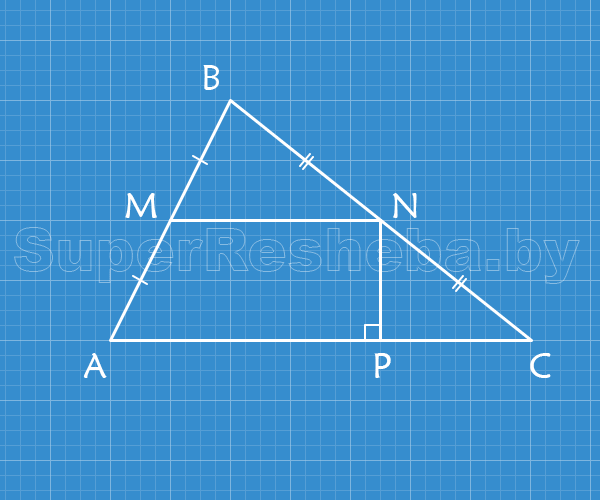
а) $ΔABC\thicksim ΔPNC;$
б) $ΔABC\thicksim ΔMBN;$
в) $ΔMBN\thicksim ΔPNC.$
Ответ: б) $ΔABC\thicksim ΔMBN.$
Вариант 2
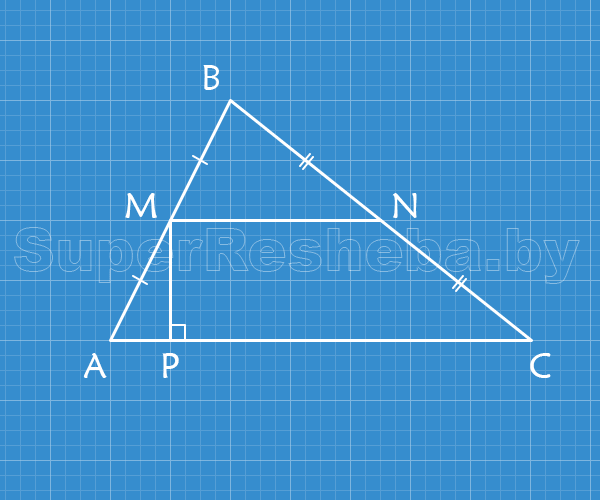
а) $ΔAMP\thicksim ΔABC;$
б) $ΔMBN\thicksim ΔABC;$
в) $ΔAMP\thicksim ΔMBN.$
Ответ: б) $ΔMBN\thicksim ΔABC.$
2.
Вариант 1
Треугольники $ABC$ и $A_1B_1C_1$ подобны, причем $∠A = ∠A_1,$ $∠B = ∠B_1.$ Назовите пары соответствующих сторон этих треугольников.
Пары: $AB$ и $A_1B_1,$ $BC$ и $B_1C_1,$ $CA$ и $C_1A_1.$
Вариант 2
Треугольники $MNK$ и $M_1N_1K_1$ подобны, причем $∠M = ∠M_1,$ $∠K = ∠K_1.$ Назовите пары соответствующих сторон этих треугольников.
Пары: $MN$ и $M_1N_1,$ $MK$ и $M_1K_1,$ $NK$ и $N_1K_1.$
3. В одном равнобедренном треугольнике угол при вершине равен $24°$ [2 в.: $38°$], а в другом равнобедренном треугольнике угол при основании равен $78°$ [2 в.: $71°$]. Докажите, что эти треугольники подобны.
Вариант 1
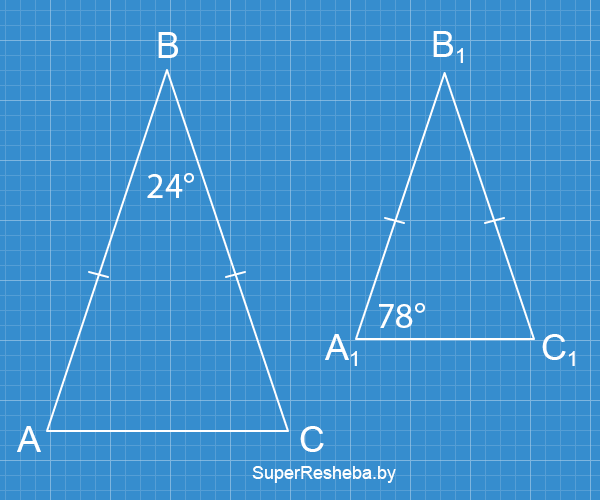
- $∠A_1B_1C_1$ $= 180° - (78° + 78°) = 24°.$
- $AB = BC,$ $A_1B_1 = B_1C_1,$ $∠ABC = ∠A_1B_1C_1$ — значит, $ΔABC \thicksim ΔA_1B_1C_1.$
Вариант 2
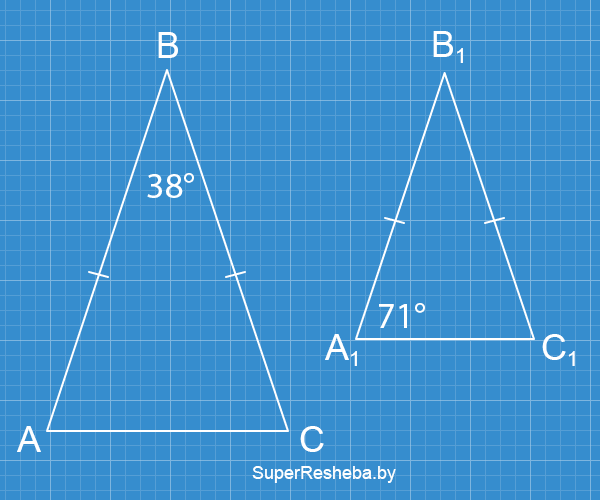
- $∠A_1B_1C_1$ $= 180° - (71° + 71°) = 38°.$
- $AB = BC,$ $A_1B_1 = B_1C_1,$ $∠ABC = ∠A_1B_1C_1$ — значит, $ΔABC \thicksim ΔA_1B_1C_1.$
4.
Вариант 1
Пользуясь данными рисунка, найдите $MP$ и $AC$, если известно, что $\dfrac{S_{ΔABC}}{S_{ΔPMK}} = 16.$
- $\dfrac{S_{ABC}}{S_{PMK}} = 16 = 4^2,$ значит $AB:PM$ $= BC:MK$ $= AC:PK$ $= 1:4;$
- $MP = \dfrac{BA}{4} = \dfrac{12}{4} = 3\, (см),$
- $AC = PK · 4 = \sqrt{5} · 4 = 4\sqrt{5}.$
Ответ: $3$ см, $4\sqrt{5}$ см.
Вариант 2
Пользуясь данными рисунка, найдите $MK$ и $AB$, если известно, что $\dfrac{S_{ΔPMK}}{S_{ΔABC}} = \dfrac{1}{25}.$
- $\dfrac{S_{PMK}}{S_{ABC}} = \dfrac{1}{25} = \left(\dfrac{1}{5}\right)^2,$ значит $PM:AB$ $= MK:BC$ $= PK:AC$ $= 1:5;$
- $MK = \dfrac{BC}{5} = 6\, (см),$
- $AB = PM · 5 = \sqrt{29} · 5 = 5\sqrt{29}.$
Ответ: $6$ см, $5\sqrt{29}$ см.
5.
Вариант 1
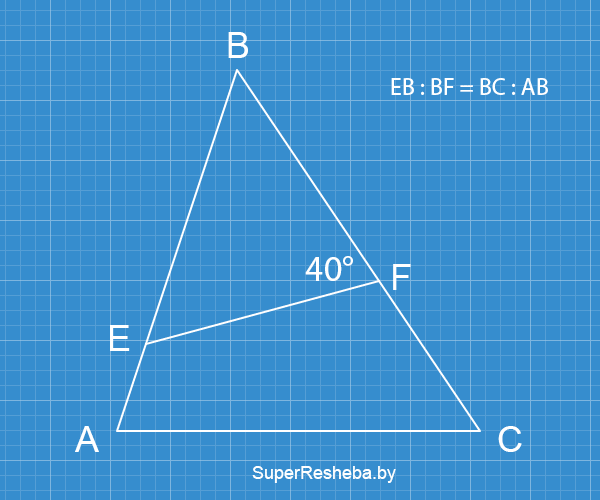
В треугольнике $ABC$ на сторонах $АB$ и $BC$ взяты соответственно точки $E$ и $F$ так, что $ЕВ : BF$ $= BC : AB,$ $∠BFE = 40°.$ Найдите угол $A.$
- $EB : BF$ $= BC : AB,$ $ΔABC$ и $ΔFEB$ имеют общий угол — значит, $ΔABC \thicksim ΔFEB;$
- $ΔABC \thicksim ΔFEB,$ значит $∠A = ∠BFE;$ $∠A = 40°.$
Ответ: $40°.$
Вариант 2
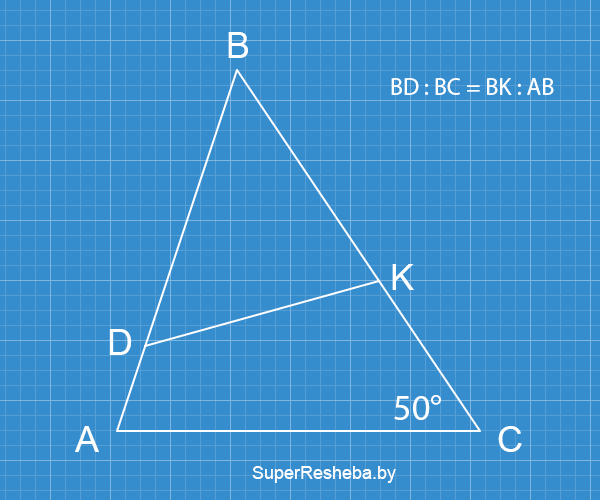
В треугольнике $ABC$ на сторонах $АB$ и $BC$ взяты соответственно точки $D$ и $K$ так, что $BD : BC$ $= BK: AB,$ $∠BCA= 40°.$ Найдите угол $BDK.$
- $BD : BC$ $= BC : AB,$ $ΔABC$ и $ΔBCB$ имеют общий угол — значит, $ΔABC \thicksim ΔBFB;$
- $ΔABC \thicksim ΔBFB,$ значит $∠C = ∠BDK;$ $∠BDK = 50°.$
Ответ: $50°.$
6.
Вариант 1
В треугольниках $ABC$ и $A_1B_1C_1$ $AB : A_1B_1$ $= BC : B_1C_1$ $= AC : A_1C_1 = 5 : 2.$ Сумма площадей этих треугольников равна $58$ см$^2$. Найдите площадь каждого треугольника.
$\dfrac{S_{ABC}}{S_{A_1B_1C_1}}=\left(\dfrac{5}{2}\right)^2=\dfrac{25}{4};$
$58:29=2$ (приходится на одну часть), значит
$S_{A_1B_1C_1}=4·2$ $=8\, (см^2);$
$S_{ABC} = 25·4=50\, (см^2).$
Ответ: $8$ см$^2$ и $50$ см$^2.$
Вариант 2
В треугольниках $ABC$ и $A_1B_1C_1 AB : A_1B_1$ $= BC : B_1C_1$ $= AC : A_1C_1.$ $S_{ΔABC}:S_{ΔA_1B_1C_1} = 9 : 16.$ $AC+A_1C_1=14$ см. Найдите длины сторон $AC$ и $A_1C_1.$
$\dfrac{S_{ABC}}{S_{A_1B_1C_1}}=\dfrac{9}{16}=\left(\dfrac{3}{4}\right)^2;$
$14:7=2$ (приходится на одну часть), значит
$AC=3·2=6\, (см^2);$
$A_1C_1=4·2=8\, (см^2).$
Ответ: $6$ см$^2$ и $8$ см$^2.$
7. Катеты прямоугольного треугольника относятся как $5 : 6$ [2 в.: $3:2$], а гипотенуза равна $122$ см [2 в.: $104$ см]. Найдите отрезки, на которые гипотенуза делится высотой, проведенной из вершины прямого угла.
Вариант 1
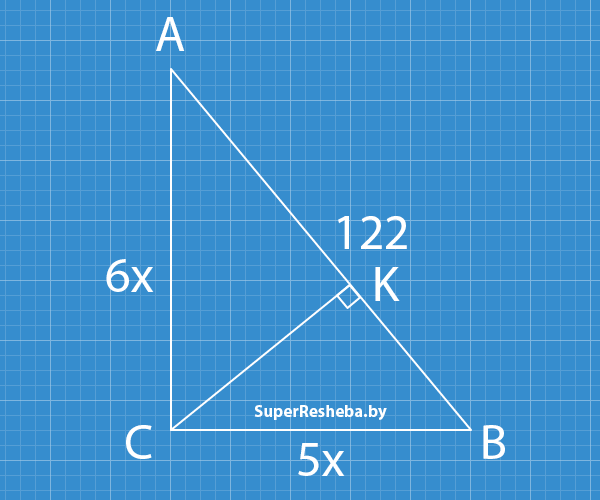
- $6^2x^2 + 5^2x^2 = 122^2;$ $x^2(36 + 25) = 122^2;$ $61x^2 = 122^2;$ $x = 2\sqrt{61};$
- $AC = 6 · 2\sqrt{61}$ $= 12\sqrt{61}\, (см),$ $CB = 5 · 2\sqrt{61} = 10\sqrt{61}\, (см);$
- $KC = \dfrac{AC · CB}{AB}$ $= \dfrac{12\sqrt{61} · 10\sqrt{61}}{122}$ $= 60\, (см);$
- $ΔAKC \thicksim ΔCKB,$ значит $\dfrac{KC}{KB} = \dfrac{AC}{CB};$ $KB = \dfrac{KC · CB}{AC}$ $= \dfrac{60 · 10\sqrt{61}}{12\sqrt{61}}$ $= 50\, (см);$
- $AK = AB - KB$ $= 122 - 50 = 72\, (см).$
Ответ: $50$ см и $72$ см.
Вариант 2
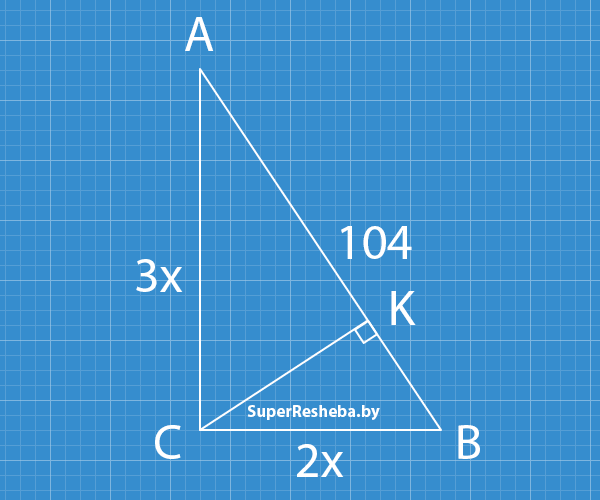
- $3^2x^2 + 2^2x^2$ $= 104^2;$ $x^2(9 + 4) = 104^2;$ $13x^2 = 104^2;$ $x = 8\sqrt{13};$
- $AC = 3 · 8\sqrt{13}$ $= 24\sqrt{13}\, (см),$ $CB = 2 · 8\sqrt{13}$ $= 16\sqrt{13}\, (см);$
- $KC = \dfrac{AC · CB}{AB}$ $= \dfrac{24\sqrt{13} · 16\sqrt{13}}{104} = 48\, (см);$
- $ΔAKC \thicksim ΔCKB,$ значит $\dfrac{KC}{KB} = \dfrac{AC}{CB};$ $KB = \dfrac{KC · CB}{AC}$ $= \dfrac{48 · 16\sqrt{13}}{24\sqrt{13}} = 32\, (см);$
- $AK = AB - KB$ $= 104 - 32$ $= 72\, (см).$
Ответ: $32$ см и $72$ см.
8. В треугольнике $ABC$ медианы $AE$ и $BP$ [2 в.: $BK$ и $CD$] пересекаются в точке $O.$ Площадь треугольника $ABC$ [2 в.: $BOC$] равна $24$ см$^2$ [2 в.: $6$ см$^2$]. Найдите площадь треугольника $AВО$ [2 в.: $ABC$].
Вариант 1
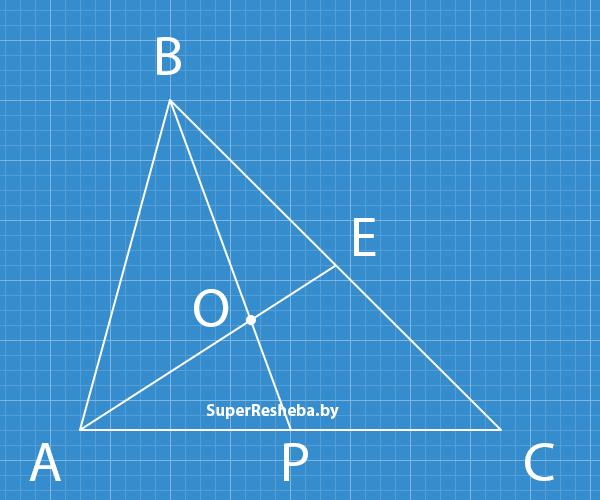
- медиана делит треугольник на две равновеликие части, значит $S_{ABE} = \dfrac{S_{ABC}}{2} = \dfrac{24}{2} = 12\, (см^2);$
- точка пересечения медиан делит их на две части в отношении $2:1,$ значит $S_{ABO} : S_{OBE} = 2:1;$
- пусть $S_{OBE} = x,$ тогда $S_{ABO} = 2x;$
$x + 2x = 12,$
$3x = 12,$
$x = 4.$
Ответ: $S_{OBE} = 8\, см^2.$
Вариант 2
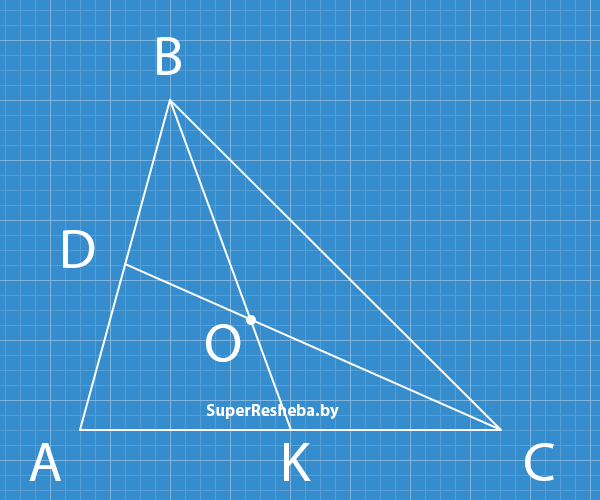
- точка пересечения медиан делит их на две части в отношении $2:1,$ значит $S_{BOC} : S_{BDO} = 2:1;$ значит $S_{BDO} = \dfrac{S_{BOC}}{2} = 3\, (см^2);$
- медиана делит треугольник на две равновеликие части, значит $S_{ABC} = S_{DBC} · 2$ $= (6 + 3) · 2 = 18\, (см^2);$
Ответ: $S_{ABC} = 18\, см^2.$
9. Отрезок $СМ$ [2 в.: $BL$] является биссектрисой треугольника $ABC.$ Известно, что $S_{ACM} = 2,$ a $S_{CBM} = 18$ [2 в.: $S_{ABL}=12,$ а $S_{CBL}=3$]. Найдите длину отрезка $BC,$ если отрезок $АС = \sqrt{7}$ [2 в.: $AB = \sqrt{13}$].
Вариант 1
- $S_{ACM} = \dfrac{AM · CH}{2},$ $S_{CBM} = \dfrac{MB · CH}{2},$ тогда $\dfrac{S_{ACM}}{S_{CBM}}$ $= \dfrac{AM}{MB},$ т. е. $\dfrac{AM}{MB} = \dfrac{2}{18} = \dfrac{1}{9}.$
- по теореме о биссектрисе треугольника получим $\dfrac{AC}{CB} = \dfrac{AM}{MB},$ тогда $BC = 9\sqrt{7}.$
Ответ: $9\sqrt{7}.$
Вариант 2
- $S_{ABL} = \dfrac{AL · CH}{2},$ $S_{CBL} = \dfrac{LC · CH}{2},$ тогда $\dfrac{S_{ABL}}{S_{CBL}} = \dfrac{AL}{LC},$ т. е. $\dfrac{AL}{LC} = \dfrac{12}{3} = 4.$
- по теореме о биссектрисе треугольника получим $\dfrac{AB}{CB} = \dfrac{AL}{LC},$ тогда $BC = \dfrac{\sqrt{13}}{4}.$
Ответ: $\dfrac{\sqrt{13}}{4}.$
10. На основании $AD$ трапеции $ABCD$ отмечена точка $K,$ причем $BK || CD$ и $CK || AB.$ Найдите отрезки, на которые разделили среднюю линию трапеции отрезки $BK$ и $CK,$ если основания трапеции равны $6$ см и $12$ см.
Вариант 1
- $AK = BC = KD = 6\, см$ (свойство параллелограмма).
- $ME = \dfrac{1}{2} · AK = 3\, см;$ $TN = \dfrac{1}{2} · KD = 3\, см;$ $TE = \dfrac{1}{2} · BC = 3\, см,$ поскольку отрезки $ME,$ $NT,$ $ET$ являются средними линиями треугольников $ABK,$ $KCD,$ $BKC$ соответственно.
Ответ: $3\, см, 3\, см, 3\, см.$
Вариант 2
На основании $BC$ трапеции $ABCD$ отмечена точка $M,$ причем $BM=MC.$ Найдите отрезки, на которые разделили среднюю линию трапеции отрезки $AM$ и $MD,$ если основания трапеции равны $8$ см и $14$ см.
Решение
- $KE = \dfrac{1}{2} · BM = 2\, см;$ $TN = \dfrac{1}{2} · MC = 2\, см,$ поскольку отрезки $KE,$ $NT$ являются средними линиями треугольников $ABK,$ $KCD,$ $BKC$ соответственно.
- $KN = \dfrac{1}{2}(BC + AD) = 11\, см$ (теорема о средней линии трапеции); $ET = KN - KE - TN = 7\, см.$
Ответ: $2\, см, 7\, см, 2\, см.$