Контр. 6. Квадратная функция
1. Из данных функций выберите квадратную:
Вариант 1
| а) $y=2x-6^2;$ | в) $y=7x^2-1;$ |
| б) $y=4x-x^3;$ | г) $y=\sqrt{x}.$ |
Ответ: в) $y=7x^2-1;$
Вариант 2
| а) $y=8x-2^2;$ | в) $y=5x+x^3;$ |
| б) $y=\sqrt{x};$ | г) $y=2x^2+6x.$ |
Ответ: г) $y=2x^2+6x.$
2. Укажите координаты вершины параболы
Вариант 1
$y = -(x + 3)^2 - 1:$
| а) $(-3;-1);$ | г) $(-3;1);$ |
| б) $(3;1);$ | д) $(0;-1).$ |
| в) $(3;-1);$ |
Ответ: а) $(-3; -1).$
Вариант 2
$y = -(x + 3)^2 - 1:$
| а) $(-4;-3);$ | г) $(-4;3);$ |
| б) $(4;3);$ | д) $(0;-3);$ |
| в) $(4;-3);$ |
Ответ: б) $(4; 3).$
3. Укажите график функции, заданной формулой
Вариант 1
$y = x2 - 5$
Ответ: а) $(-3; -1).$
Вариант 2
$y = (x+3)^2$
Ответ: б) $(4; 3).$
4. Укажите неверное утверждение:
Вариант 1
а) графиком квадратной функци является парабола;
б) функция $y=\dfrac{x^2}{3}$ является квадратной;
в) Любая парабола пересекает ось ординат;
г) множеством значений квадратной функции является множество всех действительных чисел.
Ответ: г).
Вариант 2
а) областью определения квадратной функции является множество всех действительных чисел;
б) графиком квадратной функции является гипербола;
в) ось симметрии параболы параллельна оси абсцисс;
г) график квадратной функции пересекает ось ординат в двух точках.
Ответ: а).
5. Постройте график функции
Вариант 1
$y = x^2 - 4x + 3$
| $x$ | $-1$ | $-\dfrac{1}{2}$ | $0$ | $\dfrac{1}{2}$ | $1$ |
| $y$ | $8$ | $5.25$ | $3$ | $-1.75$ | $0$ |
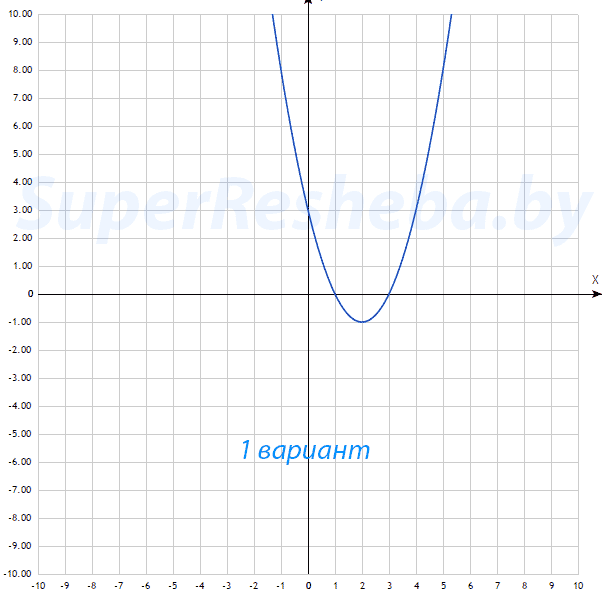
Вариант 2
$y=x^2-6x+5$
| $x$ | $-1$ | $-\dfrac{1}{2}$ | $0$ | $\dfrac{1}{2}$ | $1$ |
| $y$ | $12$ | $8.25$ | $3$ | $2.75$ | $0$ |
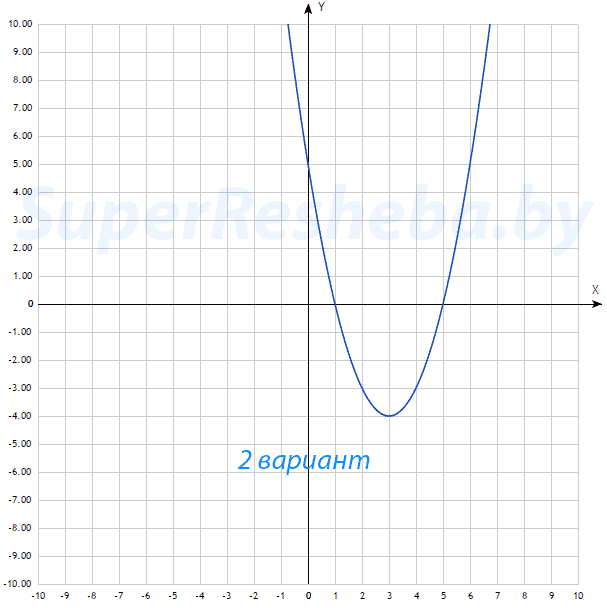
6. С помощью графика функции из задания №5 найдите:
- значения аргумента, при которых значения функции отрицательны [2 в.: положительны];
- промежуток возрастания функции [2 в.:убывания];
- уравнение оси симметрии параболы [2 в.:множество значений функции].
| Вариант 1 | Вариант 2 | |
| 1 | $(1; 3)$ | $(-∞; 1) ν (5; +∞)$ |
| 2 | $[2; +∞)$ | $(-∞; 3]$ |
| 3 | $x = 2$ | $[-4; +∞)$ |
7. Найдите нули функции, график которой получен из графика функции $y = 2x^2$ [2в.: $y=3x^2$] смещением его на три [2в.: пять] единичных отрезка вправо [2в.: влево] вдоль оси абсцисс и на восемь [2в.: три] единичных отрезков вниз вдоль оси ординат.
Вариант 1
Смещённый график на три единицы вправо и восемь единиц вниз: $y = 2(x-3)^2 - 8.$ Построим этот график и найдём нули: $1; 5.$
Вариант 2
Смещённый график на пять единиц влево и три единицы вниз: $y = 3(x+5)^2 - 3.$ Построим этот график и найдём нули: $-4; -6.$
8. Графики функции $y = ax^2$ и $y = 5 - x$ [2 в.: $y=ax^2$ и $y=1-2x$] пересекаются в точке $(2; 3)$ [2 в.: $(2;-3)$]. Найдите координаты второй точки пересечения этих графиков.
Вариант 1
$3 = 4a\, (2; 3).$
$a = \dfrac{3}{4},$
$\dfrac{3}{4} ⋅ x^2 = 5 - x,$
$3x^2 + 4x - 20 = 0.$
Находим дискриминант:
$D = 16 + 240 = 256,$
$x = \dfrac{-4 ± 16}{6},$
$x = -\dfrac{10}{3}, x = 2,$
$y = 5 + \dfrac{10}{3} = \dfrac{25}{3}.$
Ответ: $(-\dfrac{10}{3}; \dfrac{25}{3}).$
Вариант 2
$-3 = 4a\, (2; -3),$
$a = -\dfrac{3}{4},$
$-\dfrac{3}{4} ⋅ x^2 = 1 - 2x,$
$\dfrac{3}{4} ⋅ x^2 - 2x + 1 = 0.$
Находим дискриминант:
$D = 4 -3 = 1,$
$x = \dfrac{2 ± 1}{\dfrac{3}{2}},$
$x = 2, x = \dfrac{2}{3},$
$y = 1 - 2 ⋅ \dfrac{2}{3} = -\dfrac{1}{3},$
Ответ: $(\dfrac{2}{3}; -\dfrac{1}{3}).$
9.
Вариант 1
Найдите два числа, сумма которых равна 82, а произведение — наибольшее из возможных.
$x + y = 82;$
$y = 82 - x;$
$x ⋅ y = x ⋅ (82 - x)$ $= -x^2 + 82x$ $= -x^2+82x - 41^2 + 41^2$ $= -(x-41)^2 + 41^2 ≤ 41^2$ при $x є R.$
Наибольшее значение при $x = 41,$ при $y = 41.$
Вариант 2
Найдите два числа, разность которых равна 20, а произведение — наименьшее из возможных.
$x - y = 20;$
$x = y = 20;$
$x ⋅ y = (y+20) ⋅ y$ $= y^2 +20y$ $= y^2 +20y +100 - 100$ $= (y +10)^2 - 100 ≥ -100$ при $x є R.$
Наименьшее значение при $x = 10,$ при $y = -10.$
10. Постройте график функции:
Вариант 1
$y=\sqrt{x^2+8x^2+16x^2};$
$y=\sqrt{(x^2+4x)^2};$
$y=|x^2+4x|.$
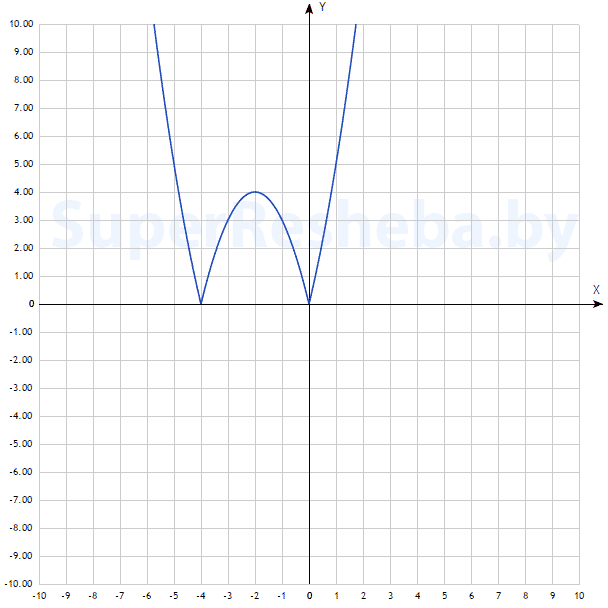
Вариант 2
$y=\sqrt{x^4-6x^3+9x^2};$
$y=\sqrt{(x^2-3x)^2};$
$y=|x^2-3x|.$