Контр. 6. Итоговая
1. Представьте 0,125 [2в.: 0,375] в виде обыкновенной дроби:
Вариант 1
| а) $\dfrac{3}{8};$ | б) $\dfrac{1}{4};$ | в) $\dfrac{1}{8};$ | г) $\dfrac{3}{4}.$ |
Ответ: в) $\dfrac{1}{8};$
Вариант 2
| а) $\dfrac{1}{4};$ | б) $\dfrac{3}{4};$ | в) $\dfrac{5}{8};$ | г) $\dfrac{3}{8}.$ |
Ответ: г) $\dfrac{3}{8}.$
2. Укажите формулу, задающую обратно пропорциональную [2в.: прямо пропорциональную] зависимость между переменными х и у:
Вариант 1
| а) $y=3x+1;$ | б) $y=6x;$ | в) $y=\dfrac{7}{x}.$ |
Ответ: в) $y=\dfrac{7}{x}.$
Вариант 2
| а) $y=5x-7;$ | б) $y=8x;$ | в) $y=\dfrac{9}{x}.$ |
Ответ: б) $y=8x.$
3. Выполните действия:
Вариант 1
$8^{-2}-\left(\dfrac{8}{9}\right)^{-1}$ $=\dfrac{1}{8^2}-\dfrac{9}{8}$ $=\dfrac{1}{64}-\dfrac{72}{64}$ $=-\dfrac{71}{64}$ $=-1\dfrac{7}{64}.$
Вариант 2
$7^{-2}-\left(\dfrac{7}{8}\right)^{-1}$ $=\dfrac{1}{7^2}-\dfrac{8}{7}$ $=\dfrac{1}{49}-\dfrac{56}{49}$ $=-\dfrac{55}{49}$ $=-1\dfrac{6}{49}.$
4. На координатной плоскости отметьте точки $K(2; -3),$ $L(2; 5),$ $M(-4; 5),$ $N(-4; -3)$ [2в.: $M(-5;4),$ $N(3;4),$ $P(3;-2),$ $Q(-5;-2)$] — вершины прямоугольника. Запишите координаты точки пересечения диагоналей прямоугольника.
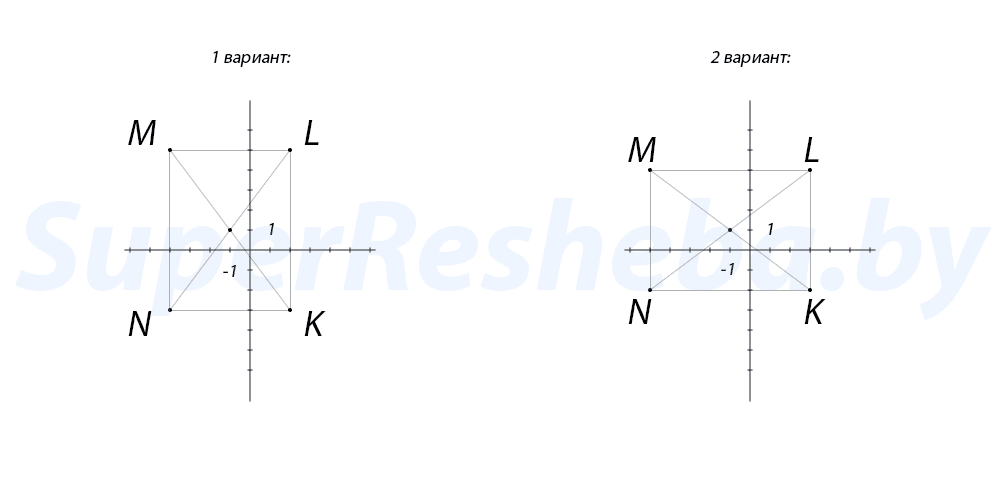
| Вариант 1 | Вариант 2 |
| Ответ: $(-1; 1).$ | Ответ: $(-1; 1).$ |
5. Найдите неизвестный член пропорции:
Вариант 1
$0.75:(-1.5)=5:x,$
$-\dfrac{0.75}{1.5}=\dfrac{5}{x},$
$x=-\dfrac{1.5·5}{0.75},$
$x=-10.$
Вариант 2
$x:3=0.16:(-4.8),$
$\dfrac{x}{3}=-\dfrac{0.16}{4.8},$
$x=-\dfrac{3·0.16}{4.8},$
$x=-0.1.$
6. Задача.
Вариант 1
При варке варенья чернику, сахар и воду берут в отношении $4:2:1$ соответственно. Сколько килограммов сахара и воды потребуется, чтобы сварить варенье из 8 кг черники?
- Пусть $x$ — это одна часть пропорции, тогда $4x = 8$ (кг черники). Найдём одну часть:
$4x = 8,$
$x = 2.$ - $2x$ — сахар, $x$ — вода.
$2 ⋅ 2 = 4$ (кг).
Ответ: $4$ кг сахара, $2$ кг воды.
Вариант 2
Для варки вишнёвого варенья было куплено 9 кг сахара. Сколько килограммов вишни и воды нужно взять, чтобы сварить варенье, если вишня, сахар и вода берутся в отношщении $4:3:1$ соответственно.
- Пусть $x$ — это одна часть пропорции, тогда $3x = 9$ (кг сахара). Найдём одну часть:
$3x = 9,$
$x = 3.$ - $4x$ — вишня, $x$ — вода.
$4 ⋅ 3 = 12$ (кг).
Ответ: $12$ кг вишни, $3$ кг воды.
7. Найдите значение выражения:
Вариант 1
$\dfrac{2\frac{7}{24}:1\frac{5}{6}-1.6·0.3}{-1.1}+(-4)^2$ $=\dfrac{\frac{55}{24}·\frac{6}{11}-\frac{4.8}{10}}{-1.1}+16$ $=\dfrac{\frac{5}{4}-\frac{4.8}{10}}{-1.1}+16$ $=\dfrac{\frac{25-9.6}{20}}{-1.1}+16$ $=-\dfrac{15.4}{22}+16$ $=-\dfrac{7.7}{11}+\dfrac{176}{11}$ $=\dfrac{168.3}{11}$ $=15.3.$
Вариант 2
$\dfrac{2.6·0.3-2\frac{4}{15}:5\frac{2}{3}}{-1.9}+(-3)^2$ $=\dfrac{\frac{7.8}{10}-\frac{34}{15}·\frac{3}{17}}{-1.9}+9$ $=\dfrac{\frac{7.8}{10}-\frac{2}{5}}{-1.9}+9$ $=\dfrac{\frac{7.8-4}{10}}{-1.9}+9$ $=-\dfrac{3.8}{19}+\dfrac{171}{19}$ $=\dfrac{167.2}{19}=8.8.$
8.
Вариант 1
В первый день комбайнеры убрали пшеницу с 0,35 поля, во второй день — с 45% поля, а в третий день — с остальных 24,6 га. Какова площадь поля?
- $0.35 = 35\%$ (поля убрали в первый день).
- $100\% — (35\% + 45\%) = 20\%$ (поля осталось убрать).
- $24.6$ составляет $20\%$ от всего поля. Пусть $x$ — всё поле, составим пропорцию:
- $\dfrac{100}{x} = \dfrac{20}{24.6}.$
$x = 100 ⋅ 24.6 : 20,$
$x = 123.$ - Ответ: $123$ га
Вариант 2
Туристы бли в походе три дня. В первый день они прошли 40 % намеченного пути, а во второй день — 0,45 пути. В третий день туристы прошли оставшиеся 6 км. Найдите длину всего пути.
- $0.45 = 45/%$ (пути было пройдено во второй день).
- $100\% — (45\% + 40\%) = 15\%$ (поля осталось убрать).
- $6$ составляет $15\%$ всего пути. Пусть $x$ — весь путь, составим пропорцию:
- $\dfrac{100}{x} = \dfrac{15}{6}.$
$x = 100 ⋅ 6 : 15,$
$x = 40.$ - Ответ: $40$ км
9.
Вариант 1
Найдите наименьшее общее кратное чисел $a$ и $b,$ если $a=\dfrac{1}{3^{-1}}·(2^{-3})^{-1}·5^2$ и $b=3^2·\dfrac{1}{5^{-2}}·2^3.$
$\dfrac{1}{3^{-1}}·(2^{-3})^{-1}·5^2$ $=3·\left(\dfrac{1}{8}\right)^{-1}·25$ $=3·8·25$ $=600;$
$3^2·\dfrac{1}{5^{-2}}·2^3 = 9·5·8=360.$
Ответ: $1800.$
Вариант 2
Найдите наибольший общий делтель чисел $a$ и $b,$ если $a=3^2·(5^{-2})^{-2}·\dfrac{1}{7^{-2}}$ и $b=3^3·\dfrac{1}{7^{-1}}·5^2.$
$3^2·(5^{-2})^{-2}·\dfrac{1}{7^{-2}}$ $=9·\left(\dfrac{1}{25}\right)^{-2}·49$ $=9·625·49$ $=275625;$
$3^3·\dfrac{1}{7^{-1}}·5^2 = 27 ·7·25=4725.$
Ответ: $1575$.
10. Решите уравнение:
Вариант 1
$|3x+5|-2=|-4+8|,$
$|3x+5|-2=4,$
|3x+5|=6.$
| $3x+5=6,$ $3x=1,$ $x=\dfrac{1}{3}.$ | $3x+5=-6,$ $3x=-11,$ $x=-3\dfrac{2}{3}.$ |
Ответ: $\dfrac{1}{3},$ $-3\dfrac{2}{3}.$
Вариант 2
$|2x-3|+5=|-5+12|,$
$|2x-3|+5=7,$
$|2x-3|=2.$
| $2x-3=2,$ $2x=5,$ $x=\dfrac{5}{2}.$ | $2x-3=-2,$ $2x=1,$ $x=\dfrac{1}{2}.$ |
Ответ: $\dfrac{5}{2},$ $\dfrac{1}{2}.$