Контр. 5. Степень с целым показателем
1. Выпишите число, представленное в стандартном виде.
| Вариант 1 | Вариант 2 |
| а) $0.1 · 10^{-5};$ б) $18 · 10^6;$ в) $9.3 · 10^9;$ г) $\frac{1}{5} · 10^3.$ | а) $\frac{1}{2} \cdot 10^{7};$ б) $7.3 · 10^5;$ в) $0.56\cdot 10^{-4};$ г) $45\cdot 10^{-5}.$ |
| Ответ: в) $9.3 · 10^9$ | Ответ: б) $7.3 · 10^5$ |
2. Укажите верное равенство:
| Вариант 1 | Вариант 2 |
| а) $3^{-2}=-6;$ б) $3^{-2}=-\frac{2}{3};$ в) $3^{-2}=-9;$ г) $3^{-2}=\frac{1}{9}.$ | а) $5^{-2}=-25;$ б) $5^{-2}=-10;$ в) $5^{-2}=\frac{1}{25};$ г) $5^{-2}=-\frac{2}{5}.$ |
| Ответ: г) $3^{-2}=\frac{1}{9}.$ | Ответ: в) $5^{-2}=\frac{1}{25};$ |
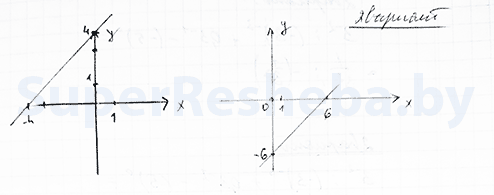
3. Укажите номер рисунка, на котором изображён график линейной функции зависимости $y = x + 4$ [2в.: $y = x - 6$].
| Вариант 1 | Вариант 2 |
| Ответ: б) | Ответ: в) |
 | |
4. Найдите площадь круга, если его диаметр равен 4 см [2в.: 6 см] (число $\pi$ окружите до сотых).
Вариант 1
- $r=\dfrac{d}{2}=\dfrac{4}{2}=2$ (см) — радиус;
- $S_{кр}=\pi r^2 = 3.14\cdot 2^2=12.56$ (см$^2$).
Ответ: $12.53$ см$^2$.
Вариант 2
- $r=\dfrac{d}{2}=\dfrac{6}{2}=3$ (см) — радиус;
- $S_{кр}=\pi r^2 = 3.14\cdot 3^2=28.26$ (см$^2$).
Ответ: $28.26$ см$^2$.
5. Выполните действие.
Вариант 1
$4^{-2}:\left(-4\right)^{-3}+0.4^{-1}-\left(-3\right)^0=$ $\dfrac{1}{16}:\left(-\dfrac{1}{64}\right)+\dfrac{1}{0.4}-1=$ $\dfrac{16} · \left(-\dfrac{64}{1}\right)+2.5-1=$ $-4+1.5=-2.5$
Вариант 2
$3^{-2}:\left(-3\right)^{-3}+0.3^{-1}-\left(-5\right)^0=$ $\dfrac{1}{3^2}:\left(-\dfrac{1}{3^3}\right)+\dfrac{1}{0.3}-1=$ $\dfrac{1}{3^2}·\left(-\dfrac{3^3}{1}\right)+\dfrac{1}{0.3}-\dfrac{0.3}{0.3}=$ $-3+\dfrac{0.7}{0.3}=\dfrac{0.9}{0.3}+\dfrac{0.7}{0.3}=$ $\dfrac{2}{3}.$
6. Ответьте на координатной плоскости вершины $A(-4; 2)$, $B(-4; 6)$ и $C(2; 6)$ [2в.: $A(-3; 1)$, $B(-3; 7)$ и $C(6; 7)$] прямоугольника $ABCD$. Найдите координаты вершины $D$.
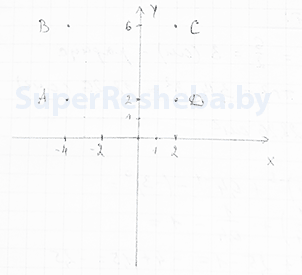
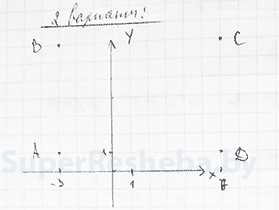
7. Упростите выражение $\frac{(a^3)^{-2}·(a^{-7})^{-1}}{a^{-3}}$ [2в.: $\frac{(a^{-2})^{-4}·(a^{3})^{-2}}{a^{-2}}$] и найдите его значение при $\alpha= 0.2$ [2в.: $0.3$].
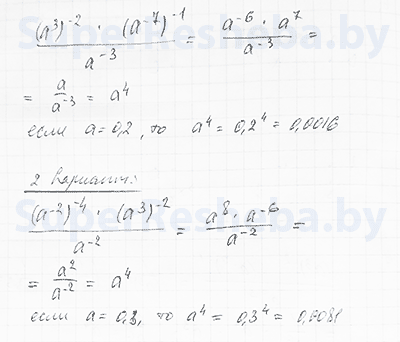
8. Известно, что график прямой пропорциональности проходит через точку $B(-6; 1)$ [2в.: $A(-4; 1)$]. Изобразите этот график.
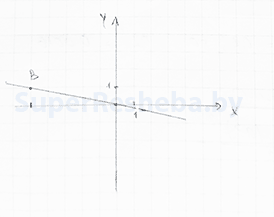
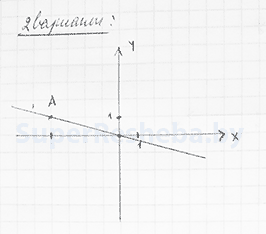
9. Найдите значение $n$, удовлетворяющие условию $7^{-13}·7^{18}:7^{n}=\frac{1}{7}$ [2в.: $5^{-19}·5^{13}:5^{n}=\frac{1}{5}$].
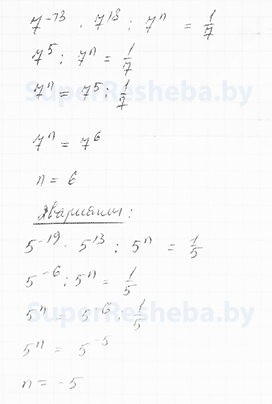
10. Отметьте на координатной плоскости все точки, у которых абсцисса и ордината — неположительные [2в.: неотрицательные] числа и их сумма равна $-5$ [2в.: $6$]. Какую фигуру образуют эти точки?
