Контр. 5. Параллельные прямые

1. Пользуясь данными рисунка, выберите верное утверждение:

Вариант 1

• а) углы $1$ и $2$ являются накрестлежащими;
• б) углы $1$ и $2$ являются односторонними;
• в) углы $1$ и $2$ являются соответственными;
• г) углы $1$ и $2$ являются вертикальными.

Ответ: б)

Вариант 2

• а) углы $1$ и $2$ являются накрестлежащими;
• б) углы $1$ и $2$ являются односторонними;
• в) углы $1$ и $2$ являются соответственными;
• г) углы $1$ и $2$ являются вертикальными.

Ответ: а)

2. Пользуясь данными рисунка, найдите расстояние от точки $A$ [2в.: $C$] до прямой $a$ [2в.: $c$].

Вариант 1

$AH = 4$ ($AH$ — расстояние от точки до прямой, т. к. является перпендикуляром между ними).

Ответ: $4.$

Вариант 2

$CH = 12$ ($CH$ — расстояние от точки до прямой, т. к. является перпендикуляром).

Ответ: $12.$

3. Две параллельные прямые пересечены третьей прямой, найдите $∠3$, если известно, что $∠1 : ∠2 = 5 : 1$ [2в.: $∠1 : ∠2 = 5 : 1$].

Вариант 1

$∠2 = 180° : 6$ (т. к. при параллельных прямых сумма односторонних углов равна $180°$). $∠2$ и $∠3$ — вертикальные, значит $∠3 = ∠2 = 30°.$

Ответ: $30°.$

Вариант 2

$∠2 = 180° : 9 · 2 = 40°$ (т. к. при параллельных прямых сумма односторонних углов равна $180°$). $∠2$ и $∠3$ — накрест лежащие, значит $∠3 = ∠2 = 40°.$

Ответ: $40°.$

4. Пользуясь данными рисунка, найдите угол $x.$

Вариант 1

Т. к. накрест лежащие углы равны, то прямые параллельны, а соответственные углы при параллельных прямых также равны, значит $∠x = 137°.$

Ответ: $137°.$

Вариант 2

Соответственные углы равны, значит прямые являются параллельными. Накрест лежащие углы при параллельных прямых также равны, значит $∠x = 53°.$

Ответ: $53°.$

5. При пересечении двух параллельных прямых третьей один из углов оказался равным $112°$ [2в.: $74°$]. Найдите наименьший [2в.: наибольший] из всех образовавшихся при этом углов.

Вариант 1

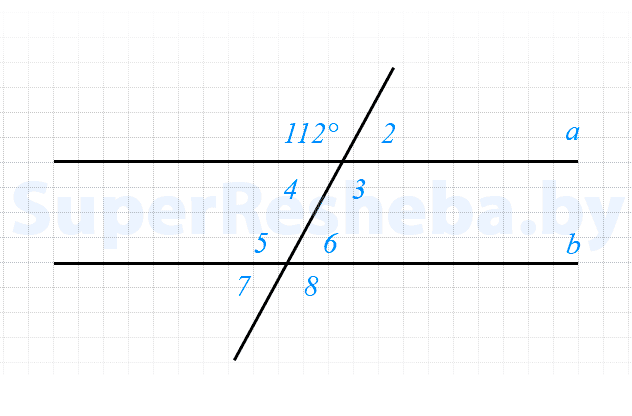
1. $∠2 = ∠4 = ∠6$ $= ∠7 = 180° — 112° = 68°,$
2. $∠1 = ∠3 = ∠5 = ∠8 = 112°.$

Ответ: $68°.$

Вариант 2

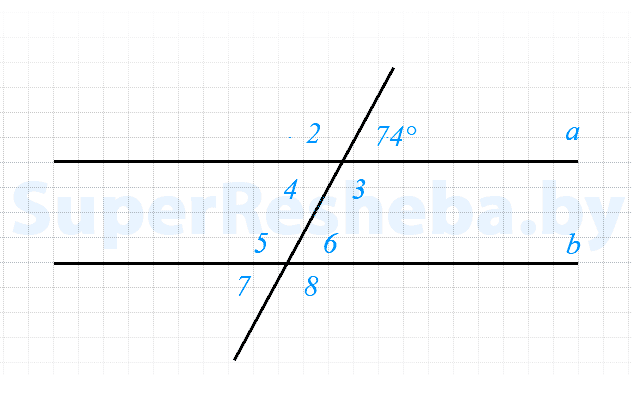
1. $∠2 = ∠3 = ∠5$ $= ∠8 = 180° — 74° = 106°,$
2. $∠1 = ∠4 = ∠6 = ∠7 = 74°.$

Ответ: $106°.$

6.

Вариант 1

На рисунке $∠1 = 43°,$ а $∠2 = 137°.$ Найдите угол $∠4$, если он больше $∠3$ на $24°.$

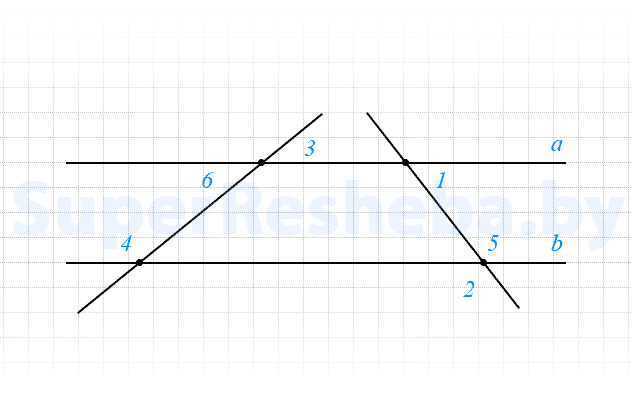
1. $∠5 = ∠2 = 137°;$
2. $∠1 + ∠5 = 43° + 137° = 180°,$ значит $a || b;$
3. $∠6 = ∠3,$ а $∠6$ и $∠4$ — односторонние при параллельных прямых, тогда;
   $∠4 + ∠6 = ∠4 + ∠3 = 180°,$ т. е. $∠3 + 24° + ∠3 = 180°,$ из этого следует, что $2 · ∠3 = 156°; ∠3 = \dfrac{156°}{2} = 78°;$
4. $∠4 = ∠3 + 24° = 78° + 24° = 102°.$

Ответ: $102°.$

Вариант 2

На рисунке $∠3 = 47°,$ а $∠4 = 133°.$ Найдите угол $∠1$, если он меньше $∠2$ на $58°.$

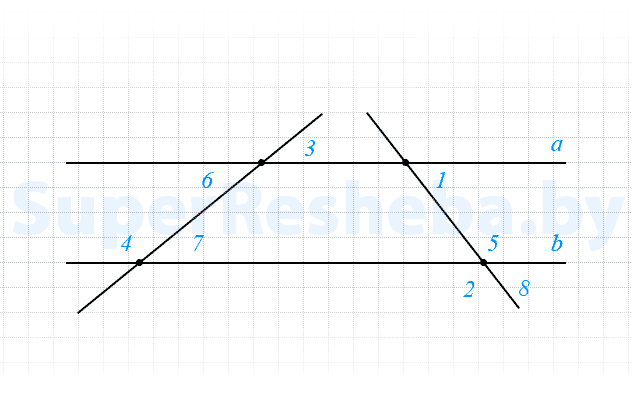
1. $∠7 = ∠3 = 47°,$ $∠4 + ∠7 = 47° + 133° = 180,$ значит $a || b;$
2. $∠5 = ∠2,$ а $∠5$ и $∠1$ — односторонние при параллельных прямых, тогда;
   $∠1 + ∠5 = ∠1 + ∠2 = 180°,$ т. е. $∠2 - 58° + ∠2 = 180°,$ $2 · ∠2 - 58­° = 180°,$ $∠2 = 119°;$
3. $∠1 = 180° -∠2 = 61°.$

Отвтет: $61°.$

7. Прямые $b$ и $a$ не имеют общих точек. На прямой $b$ отложен отрезок $MK = 81$ см [2в.: $29$ см]. На прямой $a$ отмечена точка $E$ [2в.: $P$] так, что отрезок $KE$ [2в.: $MP$] перпендикулярен прямой $a$ [2в.: $b$] и $∠KEM = 45°$ [2в.: $∠KPM=45°$]. Найдите расстояние между прямыми $b$ и $a.$

Вариант 1

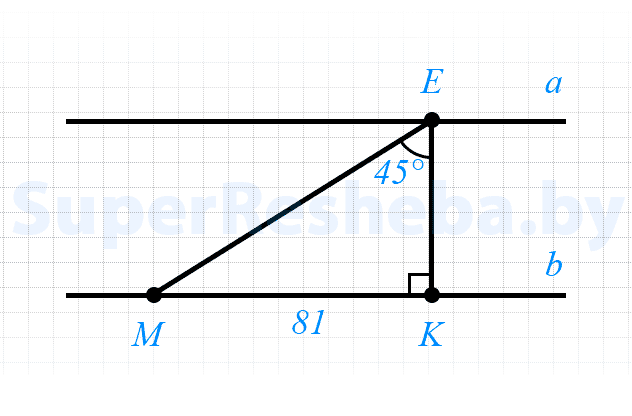
1. $a$ и $b$ не имеют общих точек, значит $a || b;$
2. $EK ⊥ a,$ значит $EK ⊥ b;$
3. $∠EMK = 180° - (90° + 45°) = 45°,$ значит $ΔEMK$ — равнобедренный, $EK = MK = 81$ см.

Ответ: $81$ см.

Вариант 2

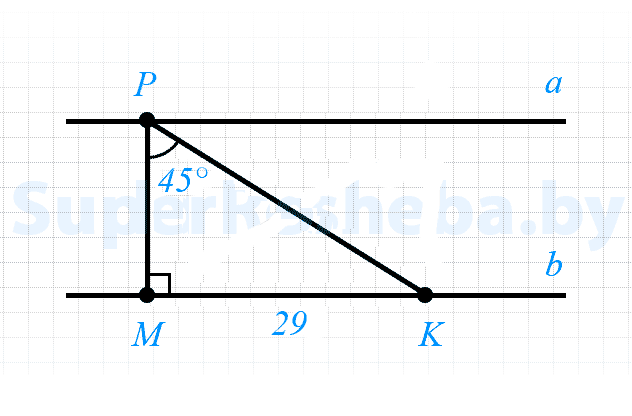
1. $a$ и $b$ не имеют общих точек, значит $a || b;$
2. $PK ⊥ a,$ значит $PK ⊥ b;$
3. $∠PMK = 180° - (90° + 45°) = 45°,$ значит $ΔPMK$ — равнобедренный, $PM = MK = 29$ см.

Ответ: $29$ см.

8. Дан угол $ABC,$ равный $76°.$ Через точку $A$ проведена прямая, параллельная прямой $BC$ и пересекающая биссектрису угла $ABC$ в точке $M.$ Найдите углы треугольника $ABM.$

Вариант 1

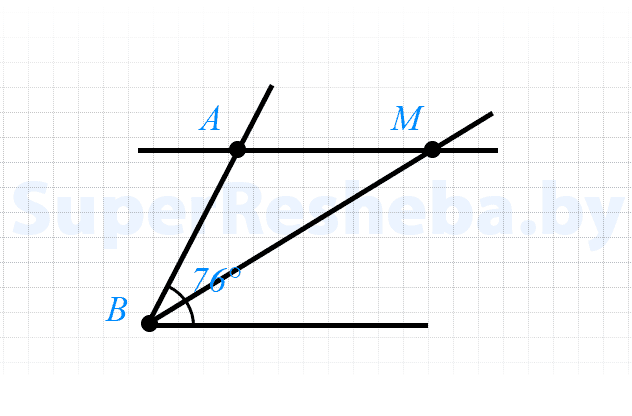
1. $∠MAB$ и $∠ABC$ — односторонние, значит $∠MAB = 180° - 76° = 104°;$
2. $∠ABM = 76° : 2 = 38°,$ т. к. биссектриса делит угол пополам;
3. $∠BMA = 180° - (104° + 38°) = 38°.$

Ответ: $104°, 38°, 38°.$

9. В равнобедренном треугольнике $BCK$ с основанием $BK$ угол при вершине $C$ равен $150°,$ а сторона $CK$ равна $12$ см. Найдите расстояние от точки $B$ до прямой $KC.$

Вариант 1

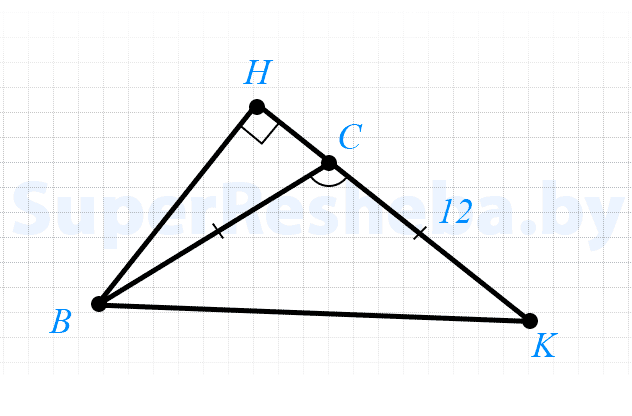
1. $ΔBCK$ — равнобедренный, значит $CB = CK = 12$ см;
2. $∠HCB$ и $∠KCB$ — смежные, значит $∠HCB = 180° - 150° = 30°;$
3. $ΔHCB$ — прямоугольный, а $∠HCB = 30°,$ то $BH = \dfrac{1}{2} · BC = \dfrac{1}{2} · 12 = 6$ см.

Ответ: $6$ см.

10. Треугольник $ABC,$ изображённый на рисунке, является равнобедренным с основанием $AC.$ Известно, что $ED = AE, ∠C = 80°,$ $∠DAC = 40°.$ Докажите, что прямые $ED$ и $AC$ параллельны. Найдите угол $BED.$

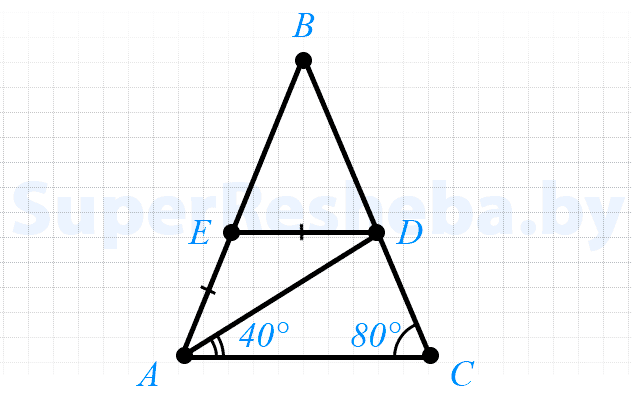
1. $ΔABC$ — равнобедренный, значит $∠C = ∠A,$ тогда $∠EAD = 80° - ∠DAC$ $= 80° - 40° = 40°;$
2. $ΔEDA$ — равнобедренный, значит $∠EAD = ∠EDA = 40°;$
3. $∠EAD$ и $∠EDA$ — накрест лежащие, значит $ED || AC.$