Урок 10

1. Закончите предложения

..., которая равна среднему расстоянию от Земли до Солнца.

1 а.е. = 149 600 000 км

..., где S = 1/2·ct, где S — расстояние до объекта, c — скорость света, t — время прохождения светила.

2. Дайте определения понятиям «параллакс» и «базис»; на рисунке 10.1 покажите эти величины

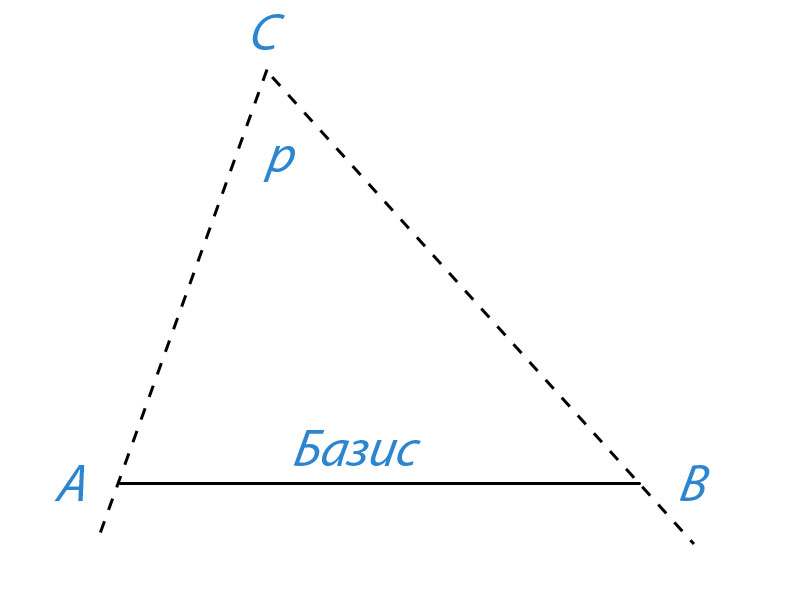
Параллакс — угол p, под которым из недоступного места (точка C) будет виден отрезок AB, называемый базисом.

Базис — тщательно измеренное расстояние от точки A (наблюдатель) до какой-либо достигнутой для наблюдения точки B.

3. Как с помощью понятий параллакса и базиса определить расстояние до удаленного недоступного объекта С (рис. 10.1)?

По величине базиса и прилегающим к нему углам треугольника ABC найти расстояние AC. При измерениях на Земле этот метод называют триангуляцией.

5. Дополните рисунок 10.3 необходимыми построениями и выведите формулу, позволяющую определить радиус небесного светила (в радиусах Земли), если известны угловой радиус светила p и его горизонтальный параллакс p

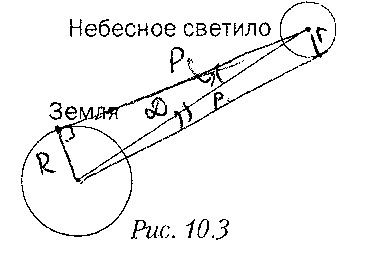
r = D · sin(ρ); R = D · sin(ρ)/sin(p) · R; r = ρ/p · R.

6. Решите следующие задачи (при расчетах считайте, что c = 3 · 105 км/с, R3 = 6370 км)

Вариант 2.

1.

Ответ: 41 млн км.

2.

Ответ: 1,22 млн км.

3.

Ответ: 3390 км.